Wissenschaftstheorie und Wahrscheinlichkeit
Statistische Bestimmung
Einführung
Die bisher erörterten Bestimmungsmethoden kommen ohne den Begriff der Wahrscheinlichkeit aus. Es gibt aber viele Bereiche, in denen diese Bestimmungsmethoden nicht funktionieren:
- Es kann zu wenig Fakten geben, um eine Bestimmung durchzuführen oder die Hypothesen können zu vage formuliert sein.
- Es kann aber auch sein, dass eine sichere Vorhersage grundsätzlich nicht möglich ist. Dies liegt an der Welt der Ereignisse. Eine Ursache – ein Ereignis – kann mehrere, sich ausschließende Wirkungen haben. Nur eine Wirkung tritt ein, aber andere Wirkungen hätten ebenfalls real eintreten können. Diese Wirkungen können nur als wahrscheinlich angesehen werden, so lange keine davon tatsächlich eingetreten ist. Bei der Formulierung, dass etwas eine bestimmte Wahrscheinlichkeit hat, muss erstens einigermaßen klar sein, welcher Entität die Wahrscheinlichkeit zugeschrieben wird und zweitens in welchem Bereich die Entität liegt.
Statistische Grundbegriffe
Um eine bestimmte Wahrscheinlichkeit zu untersuchen, wird ein satzartiger Ausdruck mit einer Variablen verwendet, der eine Menge von Ereignissen bezeichnet. Wenn die Variable durch einen «Namen» ersetzt wird, erhalten wir einen variablenfreien Ausdruck, welcher ein «echtes» Ereignis beschreibt. In der Wahrscheinlichkeitstheorie bilden Ereignisse und Ereignismengen die Grundelemente, aus denen die Modelle der Wahrscheinlichkeitstheorie konstruiert werden können. Diese Modelle werden Wahrscheinlichkeitsräume oder kurz W-Räume genannt.
Inzwischen gibt es zwei verschiedene Formulierungen der Wahrscheinlichkeitstheorie. Im «klassischen» Originalansatz, den wir hier verwenden, wird einer Entität, einem so genannten Zufallsereignis (random event), eine Wahrscheinlichkeit zugesprochen. Ein Zufallsereignis ist mengentheoretisch gesprochen eine Menge von konkreten, realen oder nur möglichen Ereignissen. All die Ereignisse aus einer solchen Menge sind sich ähnlich; sie sind durch dieselbe Formel beschrieben. Diese Ereignisse unterscheiden sich bei einer Beschreibung nur in einer einzigen Eigenschaft. Auf Sprachebene kann ein Ereignis durch einen deutschen, grammatisch korrekten Satz ausgedrückt werden. Dagegen wird ein Zufallsereignis durch eine Formel beschrieben, die eine freie Variable enthält.
Die Elemente aus einem Zufallsereignis nennen wir Elementarereignisse. Um hier drohenden Mehrdeutigkeiten zuvorzukommen, vermeiden wir in wahrscheinlichkeitstheoretischen Kontexten das Wort «Ereignis» und verwenden in solchen Zusammenhängen immer das Wort «Elementarereignis». Ein «normales» Ereignis wird also bei der Diskussion von Wahrscheinlichkeiten ein Elementarereignis und ein Zufallsereignis wird als eine Menge von Elementarereignissen betrachtet.
Im Allgemeinen wird eine Funktion eingeführt, die jedem Elementarereignis eine reelle Zahl zuordnet. Diese Funktion spielt in der Wahrscheinlichkeitstheorie eine Schlüsselrolle; sie wird Zufallsvariable genannt. Dass es sich um eine Variable handelt, sieht man daran, dass sich die Elementarereignisse in einer Menge von möglichen, zufällig stattfindenden Ereignissen befinden. So lange keines der erwarteten Elementarereignisse stattgefunden hat, werden sie variabel behandelt und untersucht. Auf der Beschreibungsebene wird eine Variable verwendet, die über die verschiedenen möglichen Elementarereignisse läuft.
Beispiel: Demokratische Wahl des Präsidenten der USA
Randbedingungen:
- Bei dieser Wahl gibt es meist nur zwei Kandidaten aus den beiden großen Politiklagern, die wir A und B nennen.
- Ein Wähler hat genau eine Stimme und die Stimmabgabe ist geheim.
- Aus Einfachheitsgründen wird das für Nicht-US Bürger etwas merkwürdige System der Wahlmänner unberücksichtigt gelassen und zusätzlich gefordert, dass jeder Wähler seine Stimme abgeben muss und dass er genau einen der beiden Kandidaten wählen muss.
Bei einer solchen Wahl gibt es eine feste Anzahl n von Wählern. Bei einer Stimmabgabe gibt es also nur zwei Möglichkeiten: ein Wähler w wählt Kandidat A oder w wählt Kandidat B. Die Wahrscheinlichkeitstheorie lässt sich dabei auf verschiedene Weise ins Spiel bringen. Dies hängt unter anderem von den Ereignisarten ab, die man bei einer Beschreibung einer Wahl verwendet. Man könnte zum Beispiel fragen:
(a) Wählen k Wähler den Kandidaten A?
(b) Gewinnt A mit einer Mehrheit von Wahlstimmen?
(c) Stimmt Wähler w für Kandidat A?
Mögliche Wahlresultate und eine Stichprobe
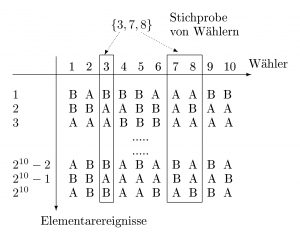
Mögliche Wahlresultate und Elementarereignisse
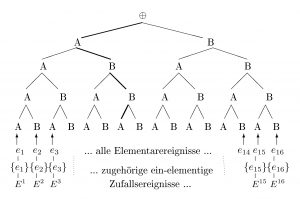
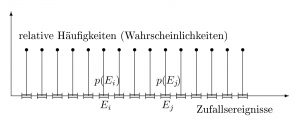
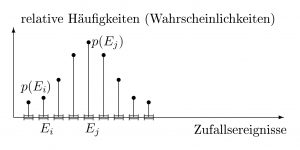
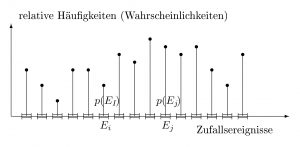
Verteilung von Elementarereignissen
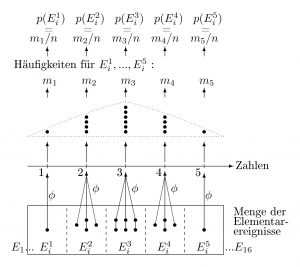
Gleichverteilte, zufällige, binomiale und stetige Verteilungen
Gleich und diskret verteilt
| Binomial verteilt
| |
Zufällig und diskret verteilt
| Stetig verteilt
|