Struktur und Invarianz
Struktur eines Modells und einer Modellklasse
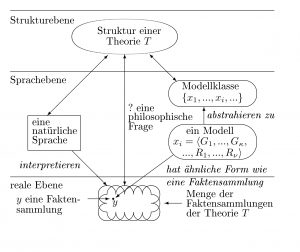
Struktur der Modelle einer Theorie
Die Struktur der Modelle einer Theorie enthält zwei Teile, nämlich erstens drei natürliche Zahlen κ, μ und ν und zweitens für jede Zahl i ≤ ν eine Typisierung τi. κ ist die Anzahl der Grundmengen, μ die Anzahl der Hilfsbasismengen und ν die Anzahl der Relationen aus Modellen einer Theorie. Dabei sind κ und ν positive Zahlen, während μ auch Null sein kann.
Eine Typisierung τi ist eine kodierte Regel, welche angibt, wie Relationen der Art Nummer i aus Grundmengen und aus Hilfsbasismengen des Modells zusammengesetzt werden. Der Begriff der Typisierung nimmt in der Wissenschaftstheorie einen zentralen Platz ein.
Eine Theorie T hat immer auch eine Struktur STR. Die Struktur STR wird durch die Zahlen κ, μ, ν und die ν Typisierungen τ1, …, τν beschrieben: STR = 〈 κ, μ, ν, τ1, …, τν 〉.
Der Begriff der Struktur bezieht sich in erster Linie auf die Theorie, erst in zweiter Linie auf bestimmte Modelle. Eine Typisierung τi in einer Theorie gilt für alle Relationen, die als ( κ + μ + i )-te Komponente der Modelle zu finden sind.
Typisierte Potenzmenge
Das Verfahren der Typisierung führt zu einer großen Menge (der Potenzmenge) von Möglichkeiten, es wird aber kein bestimmtes Element aus diesen Möglichkeiten ausgewählt. Die Auswahl eines bestimmten Elements aus der typisierten Potenzmenge, bleibt an dieser Stelle völlig offen. Es hätte auch eine andere Relation aus der Potenzmenge entnommen werden können.
Somit kann man sagen, dass sich aus einem Modell dessen Struktur eindeutig ergibt, aber umgekehrt aus einer Struktur nicht das Modell, welches über diese Struktur verfügt. Ausgehend von gegebenen Grundmengen und Typisierungen legt die Struktur nur fest, in welcher Potenzmenge die Relation Ri liegt, aber nicht wie sie im Detail aussieht.
Mehr lässt sich nur sagen, wenn die Hypothesen für das Modell genauer spezifiziert werden. Fest steht, dass eine gegebene Modellklasse eine eindeutig bestimmte Struktur hat. Alle Modelle der Klasse haben dieselbe Struktur.
Kartesisches Produkt und Potenzmenge
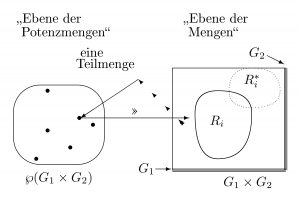
Anwendungsbereiche für den Strukturbegriff
Der so beschriebene Begriff der Struktur wird in der Wissenschaftstheorie für drei verschiedene Bereiche von Untersuchungen eingesetzt:
- In einem ersten Bereich werden verschiedene Transformationen von Modellen untersucht. Ein bestimmter Aspekt, ein Teil des Modells, bleibt bei einer Transformation gleich; eine Eigenschaft eines Modells bleibt invariant.
- In einem zweiten Anwendungsbereich der Wissenschaftstheorie wird der Strukturbegriff eingesetzt, wenn eine Struktur in mehreren Disziplinen verwendet wird. Es gibt einige Fälle, in denen zwei Modelle aus verschiedenen Theorien dieselbe Struktur haben. Es gibt auch Fälle, in denen zwei Modelle beider Theorien zwar nicht die gleiche Struktur haben, aber Teilmodelle aus beiden Theorien dieselbe (Teil-) Struktur besitzen.
- Eine weitere Anwendung des Strukturbegriffs betrifft die Übertragung der Struktur von Modellen und der Modellklassen auf die gesamte Theorie. Dieser Punkt ist wissenschaftstheoretisch interessant, weil er verschiedene Unterscheidungen und Klassifizierungen ermöglicht.