2019 SoSe – Seminarstunde 10

Theorienvergleich

Vier Dimensionen des Vergleichs

Wir unterscheiden vier Dimensionen des Vergleichs, die auch mit dem strukturalistischen Begriffsapparat beschrieben werden können. Diese vier Dimensionen bezeichnen wir wie folgt:

• Modellvergleich
• Vergleich der Faktensammlungen
• Vergleich der wissenschaftlichen Ansprüche
• Approximationsvergleich

Erste Dimension: Modellvergleich

Im Folgenden gehen wir von zwei Theorien T und T ⁰ aus, deren Komponenten wir hier auf folgende Weise abkürzen: T = 〈 STR, M, I, D, dist 〉 und T ⁰ = 〈 STR ⁰, M ⁰, I ⁰, D ⁰, dist ⁰ 〉. Ein Mo­dell x aus M hat die Form 〈 G₁, …, G_κ, A₁, …, A_μ, R₁, …, R_ν 〉 und ein Modell x ⁰ aus M ⁰ die Form 〈 G⁰₁, …, G⁰_κ⁰, A⁰₁, …, A⁰_μ⁰, R⁰₁, …, R⁰_ν⁰ 〉.

In der ersten Dimension, dem Modellvergleich, werden Modelle und die zugehörigen Hypo­the­sen der beiden Theorien verglichen.

Es werden zwei Begriffsfamilien erörtert, die mit den folgenden Termen bezeichnet werden:

• Einbettung
• Vermittlung

Modellvergleich durch Einbettung

Bei einer ersten Art von Einbettung wird ein Teil eines Modells x in einen Teil eines anderen Modells x ⁰ eingebettet. Im einfachsten Fall wird eine Grundmenge G_i von x in eine Grund­menge G⁰_j von x ⁰ eingebettet. Dazu müssen die Typisierungen der Modelle von M und M ⁰ bekannt sein. Genauer ist G_i die i-te Grundmenge von x, G⁰_j die j-te Grundmenge von x ⁰ und G_i eine echte oder unechte Teilmenge von G⁰_j, das heißt G_i ⊂ G⁰_j oder G_i ⊆ G⁰_j. Oft sind die Grund­mengen in beiden Modellen auf derselben Stelle aufgeführt: i = j ⁰. Auf dieselbe Weise lassen sich Hilfsbasismengen aus einem Modell x in Hilfsbasismengen aus einem Modell x ⁰ einbetten.

Bei einer zweiten Art von Einbettung wird eine Relation R_i aus einem Modell x von T in eine Relation R⁰_j aus einem Modell x ⁰ von T ⁰ eingebettet. In diesen Fällen müssen die Typisierun­gen τ_i und τ⁰_j der Relationen und ihre Ordnungsindizes genau angegeben werden. Genauer wird diese Einbettung wie folgt formuliert: es gibt Typisierungen τ_i und τ⁰_j , so dass es für jedes Modell x ∈ M und für jede Relation R_i der Typisierung τ_i aus x ein Modell x ⁰ ∈ M ⁰ und eine Relation R⁰_j der Typisierung τ⁰_j aus x ⁰ gibt, so dass R_i eine echte Teilmenge von R⁰_j ist, kurz: R_i ⊂ R⁰_j .

Einbettung von Komponenten zweier Modelle

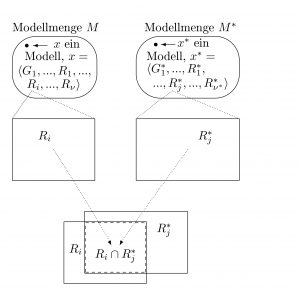
Modelle mit einer zusätzlichen Relation R^*

Modellvergleich durch Vermittlung

Bei einer Theorienvermittlung stehen die Komponenten zweier Modelle nicht in einem Teilmengenverhältnis. Zwei Kompo­nenten müssen auf eine andere Art und Weise verglichen werden; sie stehen nur noch vermit­telt in Beziehung. Die Teilmengenbeziehung wird so verallgemeinert, dass eine Komponente auf eine andere Komponente abgebildet wird. Mengentheoretisch lässt sich dies durch den Funktionsbegriff realisieren. Eine Funktion Φ wird als «Vermittler» für die Beziehung beider Kompo­nenten verwendet.

Eine erste Art von Theorienvermittlung wird als Äquivalenz von Theorien T und T ^‘ bezeich­net. Es wird auch die Bezeichnung äquivalente Darstellung verwendet. Auf Modellebene wird eine bijektive Abbildung φ zwischen den Modellmengen M und M ^‘ eingeführt. Die in­verse Abbil­dung der Funktion φ wird zum Beispiel so geschrieben: φ^. Jedes Modell x aus M wird eindeutig in ein Modell x ‘ abgebildet: x ‘ = φ ( x ) – und umgekehrt wird jedes Modell x ^‘ aus M ^‘ in ein Modell x abgebildet: x = φ ^ ( x ‘ ).

Auf der Sprachebene wird Äquivalenz durch Ableitung ausgedrückt. Die Hypothesen H von T werden durch die Hypothesen H ^‘ von T ^‘ abgeleitet – und umgekehrt. Solche Äquivalenzen findet man bis jetzt fast nur in der Mathematik und der Physik.

Zwei äquivalente Darstellungen eines Raumes

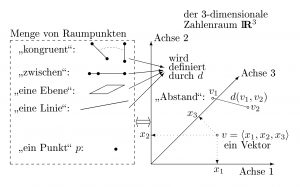
Bei einer zweiten Art von Theorienvermittlung werden nur Teile von Komponenten in Bezie­hung gesetzt. In der obigen Abbildung «Einbettung von Komponenten zweier Modelle» enthält der Durchschnitt der Relationen R_i und R^*_j viele Ele­mente. Bei einer Theorienvermittlung kann ein solcher Durchschnitt hingegen leer sein. So kann es zum Beispiel sein, dass zwei Grundmengen kein einziges Element gemeinsam haben. Durch eine Funktion werden zwei disjunkte Relationen oder Grundmengen aufeinander abge­bildet. Bei der hier erörterten Situation können wir in der obigen Abbildung die Relationen R_i und R^*_j disjunkt werden lassen und eine Funktion φ dazwischenschalten, so dass die Elemente (Er­eig­nisse) von R_i auf solche von R^*_j abgebildet werden.

Eine letzte Art von Vermittlung entsteht durch Verknüpfung. Die Zuordnung geschieht nicht durch eine Funktion allein. Ein Argument der Funktion η wird durch eine Gleichung oder durch eine andere abstrakte Beziehung in einen Funktionswert von η transformiert.

Theorienvermittlung durch Verknüpfung

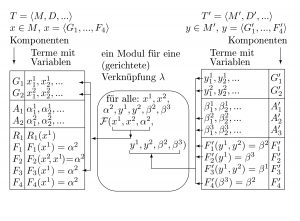
Zweite Dimension: Vergleich der Faktensammlungen

In der zweiten Dimension wird mit dem Vergleich der Faktensammlungen die Vermittlung von der Modellebene auf die Ebene der Faktensammlungen heruntergezogen. Bei einer Vermitt­lung zwischen Faktensammlungen geht es im Wesentlichen um «kleine» Mengen von realen, ele­mentaren Ereignissen. Bei einer Vermittlung zwischen Modellen geht es dagegen meist um unendlich viele Elemente, die durch Terme mit Variablen beschrieben werden. Auf Ebene der Faktensammlungen werden also Fakten in den Vordergrund gerückt, während es auf der Modellebene um Hypothesen geht.

Eine Faktensammlung besteht aus Listen von Mengen von elementaren Ereignissen und Sach­verhalten. Für eine solche Menge liegt aber kein allgemein formulierter Satz vor. Meist wird eine Komponente einer Faktensammlung wieder als eine Liste von Ereignissen, Sach­verhalten oder Objekten geführt. Jedes real untersuchte Ereignis erhält eine Bezeichnung, die das Ereignis identifiziert. Dagegen geht es in einem Modell um allgemeine, variabel ausge­drückte Ereignisse oder Sachverhalte. Der Zusammenhalt von Ereignissen entsteht erst auf der Modellebene, wenn Hypothesen für das Modell beschrieben werden.

Gemeinsame Fakten aus Faktensammlungen

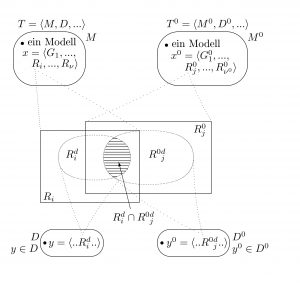
Dritte Dimension: Vergleich der wissenschaftlichen Ansprüche

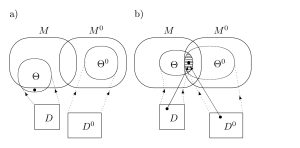
Vierte Dimension: Approximationsvergleich

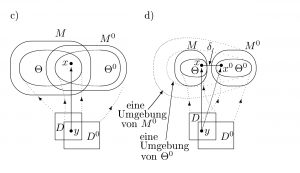
In der vierten Dimension werden die Approximationsapparate zweier Theorien verglichen.

Zwei Theorien können die gleiche Approximationsmethode verwenden. In diesem Fall lässt sich der Vergleich auf Abstandskonstanten zurückführen. Diese Konstanten hängen von der Anzahl der Faktensammlungen, der jewei­ligen Größe einzelner Faktensammlungen und von der Struktur der Modelle der Theorien ab. Wenn es in der Theorie T beispielsweise um wenige Faktensammlungen geht, kann keine Faktensammlung vernachlässigt werden. Eine Umgebungskonstante k_D für die Menge D der Fak­tensammlungen kann in diesem Fall nicht variiert werden. Nur die Umgebungskonstante k_x, die von der Anzahl der Elemente in den Grundmengen der Modelle x abhängt, lässt sich variieren. Wenn eine neue, «bessere» Theorie T ⁰ gefunden wird, müssen die Konstanten 〈 k_D, k_x 〉 mit den entsprechenden Konstanten 〈 k⁰_D⁰, k⁰_x⁰ 〉 der Theorie T ⁰ verglichen werden. Die Gewichtung der Konstanten und die Struktur der Modelle kommen ins Spiel. All dies führt in die Statistik, die für die Wissenschaftstheorie inzwischen unerlässlich geworden ist.