Sprachen und Ausdrücke
Wissenschaft und Wissenschaftstheorie werden durch Sprachen mitgeteilt und beschrieben. Ohne Sprache gibt es keine Wissenschaftstheorie. Aber sind Sprachen auch zentrale Bestandteile der Wissenschaftstheorie?
Es gibt drei Arten von Sprachen: natürliche, universale und formale Sprachen. In einer Sprache werden viele verschiedene Arten von Ausdrücken benutzt, die je nach Situation bestimmten Bereichen zugeordnet werden.
Die natürlichen Sprachen sind für die Wissenschaftstheorie durchaus relevant. Es ist aber auch klar, dass eine natürliche Sprache kein zentraler Bestandteil der Wissenschaftstheorie sein kann. Das schlagende Argument hierfür lautet: die meisten Wissenschaftler können die anderen Sprachen, in denen viele der Menschen über Wissenschaft sprechen, nicht verstehen.
Für die Wissenschaftstheorie ist es sinnvoll, zwei sprachliche Ebenen zu unterscheiden. In der universellen Ebene wird ein Sprachfragment nur für abstrakte Formen benutzt. Erst in der Ebene der vielen verschiedenen Wissenschaften und Theorien wird jeweils eine spezielle formale Sprache verwendet – je nach Anwendungsfall einer Theorie.
Für diese Vorgehensweise sind die mengentheoretischen Sprachen besonders gut geeignet. Der mengentheoretische Rahmen lässt einerseits Platz für alle wissenschaftlichen Inhalte. Dieser Rahmen kann für die Mathematik ebenso gut verwendet werden, wie für Politologie oder Hermeneutik. Auf der anderen Seite kann bei der Beschreibung eines bestimmten intendierten Systems mengentheoretisch immer weiter sowohl in abstraktere als auch in konkretere Ebenen vorgestoßen werden.
Mengentheoretische Terme sind inzwischen auch oft in der Wissenschaftstheorie anzutreffen. Terme für Entitäten wie: Modelle, intendierte Systeme, Fakten, Theorienentwicklungen, reelle Zahlen und vieles mehr – werden immer durch atomare Bestandteile konstruiert. Einige dieser atomaren Ausdrucksformen sind in der folgenden Tabelle zusammengestellt:
| a ∈ G ( oder ai ∈ Gj ) | das Objekt a liegt in der Menge G |
| a ∈ H ( oder ai ∈ Hj ) | eine Zahl a liegt in der Menge H |
| a ∈ { x / E (x) } | ein Element a liegt in der Menge, deren Elemente x die Eigenschaft E haben |
〈 a, b, c 〉 ∈ A × B × C ( oder: 〈 a1, a2, a3 〉 ∈ A1 × A2 × A3 ) | die Liste 〈 a, b, c 〉 liegt in der Menge A × B × C (dem kartesischen Produkt der Mengen A, B und C) |
〈 a, a 〉 ∈ A × H, oder ( 〈 ai, aj 〉 ∈ Ar × Hs ) | die Liste aus dem Objekt a und der Zahl a liegt in der Menge A x H |
| 〈 a1, … , an 〉 ∈ R | Relation R drückt einen Sach- verhalt zwischen a1, … , an aus |
f ( a ) ∈ B ( oder f ( ai ) ∈ B ) | der Funktionswert f ( a ) liegt in der Menge B |
| c ∈ K | die Konstante c liegt in der Menge K |
| p ( E ) = a | die Zahl a drückt aus, wie wahrscheinlich das Ereignis E ist |
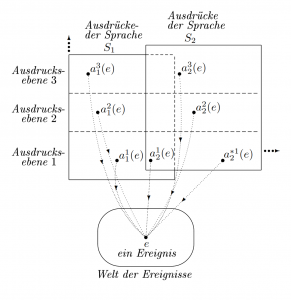
Ein Ereignis lässt sich auf viele verschiedene Weisen und in verschiedenen Sprachen ausdrücken. In der nächsten Abbildung sind Ausdrücke aus zwei natürlichen Sprachen S1, S2 zu sehen. Einige hervorgehobene Ausdrücke, die aus verschiedenen Beschreibungsebenen stammen, bezeichnen alle dasselbe reale Ereignis e. Zwei Rechtecke stellen zwei Sprachen dar, die in drei Beschreibungsebenen unterteilt sind. Die Punkte in den Rechtecken stellen Ausdrücke dar. Punkte im Oval der Abbildung sind graphisch dargestellte, reale Ereignisse. Diese Ereignisse werden normalerweise nicht wahrgenommen. Ein bestimmtes Ereignis e ist durch einen schwarzen Punkt hervorgehoben. In den Rechtecken sind einige Ausdrücke ebenfalls durch schwarze Punkte dargestellt und mit Symbolen aij(e) bezeichnet. Der untere Index j läuft über die beiden Sprachen, der obere Index i über Ausdrucksebenen. Der rechts eingezeichnete, dick gepunktete Pfeil deutet an, dass weitere Sprachen hinzugefügt werden können. Auf ähnliche Weise besagt der dick gepunktete Pfeil oben links, dass weitere Ausdrucksebenen vorhanden sein könnten. Die dünn gepunkteten Pfeile bedeuten, dass ein Ausdruck aij(e) ein bestimmtes Ereignis e bezeichnet. Im Beispiel deuten alle schwarz hervorgehobenen Ausdrücke aij(e) auf dasselbe reale Ereignis e. Das Ereignis e, welches durch die drei symbolischen Ausdrücke a11(e), a21(e), a31(e) bezeichnet wird, lässt sich in der deutschen Sprache auf verschiedene Weise ausdrücken. Auf einer ersten, technischen Ebene könnte zum Beispiel der Ausdruck Umwandlung von Kohle in Energie benutzt werden. Auf einer ökonomischen Ebene wäre der Ausdruck Produktion von Strom durch das Unternehmen RWE treffend und auf ökologischer Ebene könnte der Ausdruck Einbringen von Schadstoffen in die Atmosphäre verwendet werden. Auf ähnliche Weise lassen sich die Ausdrücke a12(e), a22(e), a32(e) in der englischen Sprache formulieren. Ein Beispiel für einen überlappenden Ausdruck a12(e) wäre zum Beispiel googeln.
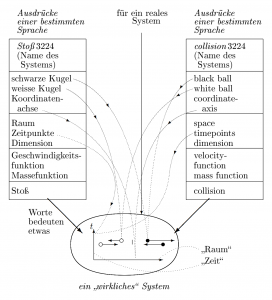
Diese linguistische Situation wird durch eine wissenschaftliche Anwendung genauer erläutert. In der folgenden Abbildung ist im unteren Bereich ein reales System aufgeführt – ein mechanischer Stoß – wie er in der klassischen Mechanik untersucht wird. Man sollte sich hierbei den gezeichneten Stoß als tatsächlich stattfindend vorstellen und ihn direkt wahrnehmen. Ein schwarz dargestelltes, „schweres” Partikel stößt mit einem weißen, „leichten” Partikel auf einer geraden Linie zusammen. Diese experimentelle Anordnung ist in der Literatur oder im Internet oft zu finden. Um die räumlichen Abstände zu messen, steht ein Stab, ein Metermaß, parallel zur Stoßebene und eine per Hand startbare Uhr bereit. Diese Uhr ist durch eine t-Achse repräsentiert.
Links oben sind die wichtigsten Ausdrücke, mit denen dieses Ereignis physikalisch beschrieben werden kann, in deutscher Sprache notiert. Rechts oben ist eine ähnliche Liste mit Ausdrücken in englischer Sprache zu sehen. Von einigen Ausdrücken führen gepunktete Pfeile zu den entsprechenden Teilen oder Teilprozessen, die im ablaufenden Stoß vorhanden sind. So deutet beispielsweise der Ausdruck schwarze Kugel auf die im Stoß zu sehende schwarze Kugel hin: der Ausdruck bezeichnet einen materielle Gegenstand. Der Ausdruck Stoß deutet auf ein Ereignis. Der Ausdruck Dimension kann nicht direkt auf etwas Konkretes hindeuten. Ein Ausdruck dieser Art wird sprachlich normalerweise auf andere Ausdrücke zurückgeführt. Der in der Abbildung eingezeichnete Pfeil unten links besagt, dass die Ausdrücke im realen System eine bestimmte Bedeutung haben.
Begriffe
Begriff: Einführung
Was ist ein Begriff?
Begriff – etymologisch vom Stammwort greifen abgeleitet – bedeutet:
- In erster Näherung eine Vorstellung einer Sache, die zum Greifen nahe ist und die durch Sprache ausgedrückt werden kann.
- In zweiter Näherung, bevor die Mengenlehre auf den Plan trat, wurde der Begriff in Umfang und Inhalt unterteilt.
- In dritter Näherung wurden schließlich auch Mengen benutzt. Der Umfang eines Begriffs wird als eine Menge vorgestellt; die Elemente dieser Menge fallen unter diesen Begriff.
Auch beim Inhalt eines Begriffs werden weitere Bestandteile, wie syntaktische, paradigmatische und semantische Elemente unterschieden. Hauptsächlich durch psychologische Untersuchungen wurde klar, dass dem Begriff ein begrifflicher Raum (conceptual space) zugeordnet werden muss, der auch mehrere Dimensionen haben kann. Zum Beispiel werden beim Begriff des Raumes normalerweise drei räumliche Dimensionen unterschieden. Bei einem anderen Ansatz, wird der Inhalt eines Begriffs durch sprachliche Ausdrücke und Konstrukte dargestellt.
Der „Tripelansatz“ von Kuznetsov
Definition
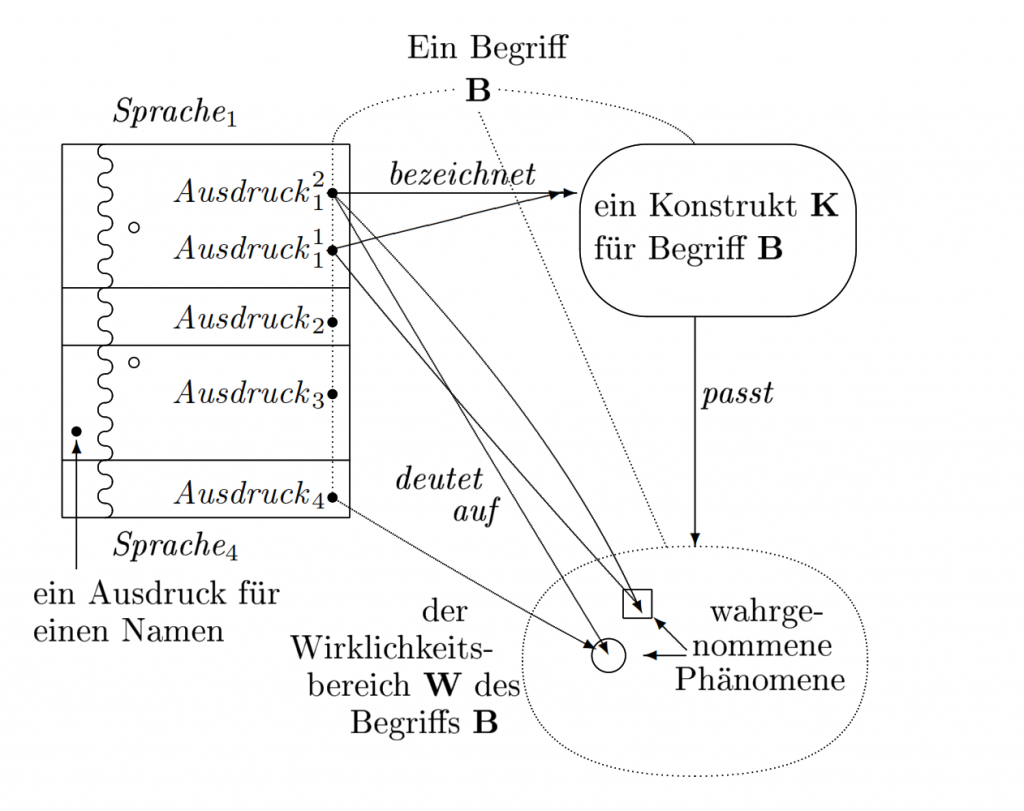
Im „Tripelansatz” von Kuznetsov besteht ein Begriff B aus drei Komponenten, nämlich aus dem Wirklichkeitsbereich W des Begriffs, aus einer Gesamtheit K von Konstrukten des Begriffs und aus einer Menge E von sprachlichen Ausdrücken (englisch: expression) für den Begriff:
B = 〈 W, K, E 〉
Diese drei Komponenten liegen in verschiedenen Dimensionen: die Ausdrücke in der Sprachdimension, die wirklichen Ereignisse in der Wirklichkeitsdimension und ein Konstrukt in der Dimension der Mengen.
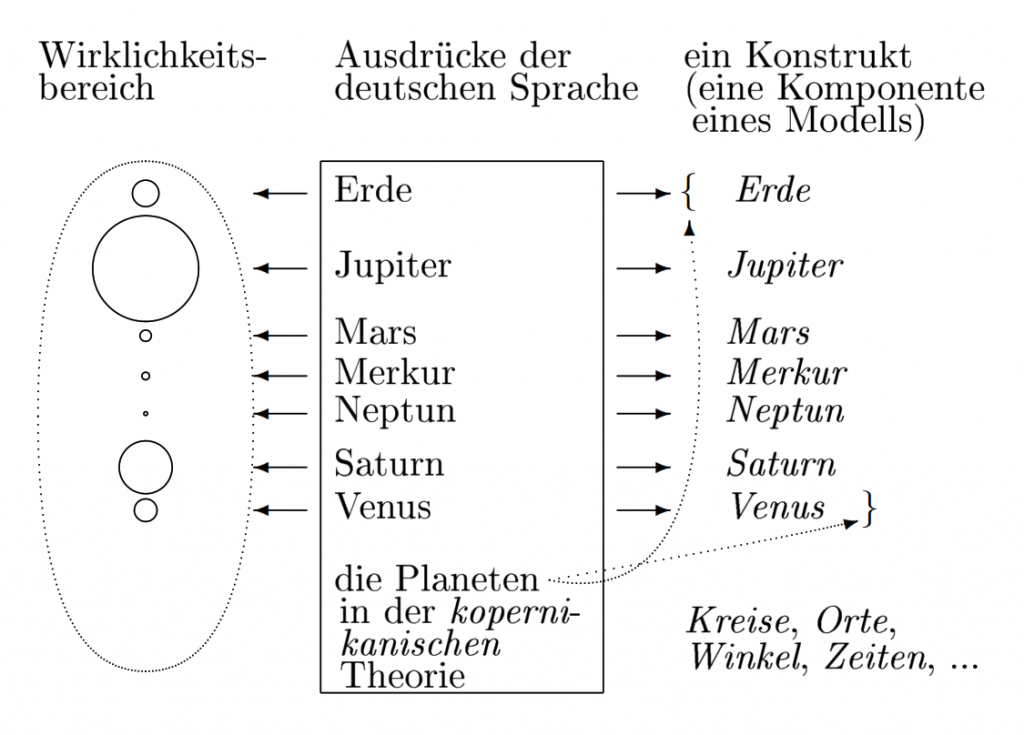
Eine Menge ist philosophisch gesehen eine Art Zwitter. Sie enthält einen Sprachanteil und einen „natürlichen” Anteil, der unabhängig von menschlicher Wahrnehmung existiert. Die Menge der Planeten zum Beispiel wird einerseits von einer Person mental erfasst und durch Worte ausgedrückt. Andererseits sind die meisten Menschen der Meinung, dass es viele verschiedene Planeten, wie zum Beispiel unsere Erde und die Venus – also eine Art von Gesamtheit – auch geben würde, wenn die Menschheit nicht existieren würde.
Der Wirklichkeitsbereich W des Begriffs besteht aus einer sehr großen Menge von Ereignissen („Phänomenen”), über die ohne Sprache nichts ausgesagt werden kann. Ein solches Ereignis ist etwas, das letztlich nur durch eine Person wahrgenommen wird oder zu einem früheren Zeitpunkt wahrgenommen wurde. Weitere abstrakte, konstruierte oder rein gedachte Phänomene lassen sich immer von den direkt wahrgenommenen Ereignissen ableiten. Zum Beispiel nimmt eine Person zu einem Zeitpunkt und an einem bestimmten Ort ein Ereignis wahr, welches sie durch den Ausdruck die Venus geht gerade auf äußert.
Ein Konstrukt aus K ist eine Komponente eines Modells einer Theorie T, wobei das Konstrukt zu einem bestimmten Begriff der Theorie T gehört. Ein Modell hat die Form
〈 G1, …, Gk, A1, …, Am, R1, …, Rn 〉
wobei G1, …, Gk die Grundmengen, A1, …, Am die Hilfsbasismengen und R1, …, Rn die Relationen des Modells sind. Ein Konstrukt kann die Form einer Grundmenge oder einer Relation des Modells haben, es kann aber auch durch die Grundmengen und Relationen definiert sein – in einfacher oder komplexer Weise.
Die dritte Komponente E eines Begriffs enthält einerseits Ausdrücke, die auf Ereignisse deuten, welche unter den Begriff fallen. Ein solcher Ausdruck kann ein Name oder eine ausführlichere Beschreibung eines Objekts oder eines Phänomens sein. Andererseits enthält E Ausdrücke, die den Begriff „als Ganzes” bezeichnen. Die Ausdrücke der letztgenannten Art bezeichnen abstrakte, allgemeine Sachverhalte. Ein solcher Ausdruck enthält zwingend auch mindestens eine Variable, nämlich für die Ereignisse, die unter diesen Begriff fallen. Unter den Ausdrücken finden wir normalsprachliche Terme, Sätze und Phrasen, wie Hartz IV; Die Erde kreist um die Sonne; oder der helle Abendstern. In wissenschaftlichen Beschreibungen spielen zusätzlich Variablen eine wichtige Rolle, mit denen verschiedene mögliche, in Wirklichkeit aber nicht stattfindende Ereignisse erörtert und beschrieben werden. Bei einem Term, einem Satz und einem Ausdruck kann man ein Substantiv eventuell an mehreren Stellen durch eine Variable ersetzt. Aus einem Satz entsteht auf diese Weise eine sogenannte Formel. Eingeschränkt auf eine bestimmte Theorie und einen bestimmten Begriff, der zu dieser Theorie gehört, lässt sich ein Ausdruck angeben, welcher die Menge aller Konstrukte des Begriffs beinhaltet. Die einzelnen Konstrukte des Begriffs sind Teile von Modellen dieser Theorie. Der so abstrakt umschriebene Bereich charakterisiert somit den Inhalt des Begriffs durch ein mengentheoretisches Prädikat.
Beziehung zwischen den drei Komponenten
Die drei Komponenten eines Begriffs werden durch drei Beziehungen zusammengehalten:
- Bei der ersten Beziehung deutet ein Ausdruck auf ein wirkliches Ereignis.
- Bei der zweiten Beziehung bezeichnet ein Ausdruck – situationsabhängig – ein Konstrukt.
- Bei der dritten Beziehung passt ein Konstrukt zu dem Wirklichkeitsbereich.
Alle drei Beziehungen werden in vielen Disziplinen, wie zum Beispiel Philosophie, Psychologie, Kognitionswissenschaft, Linguistik und Informatik genauer untersucht.
Ein Begriff B und seine drei Komponenten W, K und E.
Strukturelle Ähnlichkeit von Theorien und Begriffen
Es ist deutlich zu erkennen, dass Theorien und Begriffe strukturell ähnlich sind:
- Die Menge der Faktensammlungen einer Theorie entspricht dem Wirklichkeitsbereich eines Begriffs.
- Die Modelle entsprechen den Konstrukten.
Ein Unterschied zwischen Begriffen und Theorien besteht darin, dass bei den Begriffen die normalen Sprachen eine größere Rolle spielen als bei den Theorien.
Begriff: Beispiele
Der Begriff die Planeten in der kopernikanischen Theorie
Der Begriff des Nutzens
Dieser Begriff liegt in der Wissenschaft weit weg von der Beobachtungsebene. Einen Nutzen können wir nicht direkt wahrnehmen. Trotzdem spielt er in der heutigen Weltsicht eine zentrale Rolle; alle Handlungen der Menschen werden so gedeutet, dass sie einen möglichst großen Nutzen haben sollen. Der Begriff des Nutzens ist von einem anderen Typ als zum Beispiel der der Sonne. Nutzen ist in der Grundbedeutung eine relationale Beziehung zwischen einer Person und den Gegenständen, die sie besitzt oder besitzen möchte. Je mehr Dinge eine Person besitzt, desto mehr Nutzen kann die Person (normalerweise) aus diesen ziehen – desto mehr Nutzen hat sie. Dieser Begriff wird heute in vielen verschiedenen Bedeutungsvarianten verwendet. Sowohl der Wirklichkeitsbereich als auch das Konstrukt ist nicht einfach zu beschreiben.
In der deutschen Sprache werden Ausdrücke verwendet wie: Nutzen, Nutzenfunktion, Nutzenfunktion einer Person in einer Situation, und viele weitere. Das Substantiv Nutzen bezeichnet ein schwer verständliches, wirkliches Objekt. Über den Wirklichkeitsbereich des Begriffs lässt sich ohne Worte wenig sagen. Der Begriff bekommt mehr Inhalt, wenn wir durch die Sprache mehr über die Wirklichkeit und über ökonomische Modelle erfahren.