Modelle
Einführung und Definition
Von einem realen System zu einem Modell
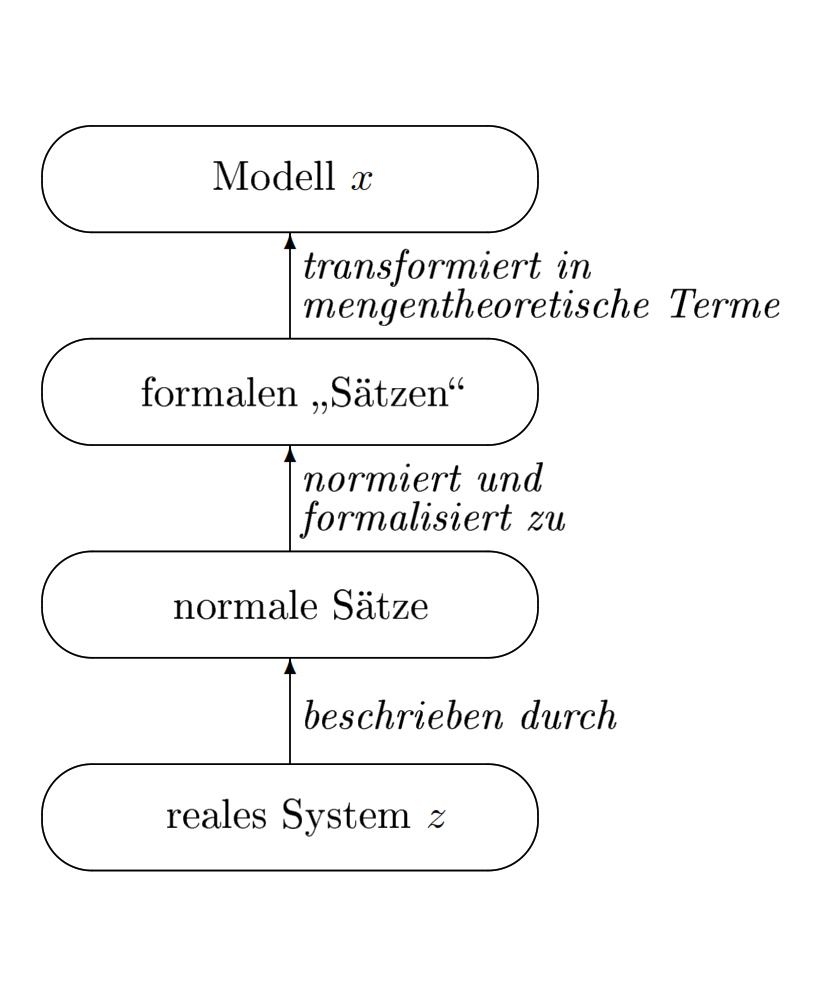
Bestandteile eines Modells
Ein Modell wird in zwei Schritten genauer beschrieben:
- Im ersten Schritt werden die Bestandteile des Modells in ihre elementaren Teile zerlegt.
- In einem zweiten Schritt lassen sich aus den elementaren Bestandteilen einfache und komplexe Teile des Modells zusammensetzen.
Einfache Bestandteile eines Modells werden Fakten und komplexe Teile Hypothesen genannt. Diese Unterscheidung wird auch auf der Beschreibungsebene getroffen.
Alle Bestandteile eines Modells werden durch Terme beschrieben: Fakten durch einfache Terme und Hypothesen durch komplexe Terme. Fakten bilden in der Wirklichkeit vorhandene Ereignisse ab, die in der gerade untersuchten Situation Grundbestandteile des Modells sind und die nicht weiter analysiert werden. Hypothesen repräsentieren Gesamtheiten von Ereignissen, die in einem Modell eine Einheit bilden.
Definition eines Modells
Ein Modell ist eine Liste von Mengen. Eine solche Menge nennen wir auch eine Komponente (des Modells, der Liste). Es werden drei Arten von Mengen in einem Modell unterschieden: Basismengen, Hilfsbasismengen und Relationen:
Eine Basismenge enthält Objekte oder Dinge oder auch elementare Ereignisse. Ereignisse nennen wir elementar, wenn sie für die Theorie nicht weiter in kleinere Einzelteile zerlegt werden.
Eine Hilfsbasismenge besteht aus mathematischen Objekten (Zahlen oder abstrakteren Dingen).
Eine Relation R ist eine Menge von Listen, die durch eine „Bezeichnung“ (z.B. durch ein Prädikatsymbol) der Relation zusammengehalten wird. Ein Element einer Relation besteht aus einer Liste von Variablen, die verschiedene Typen haben können. Eine solche Variable läuft über einen Bereich. Der Bereich enthält Fakten und auch „mögliche Fakten“.
Z.B. ist p die Bezeichnung (das Prädikatssymbol) und fakt1, …, faktn sind mögliche Fakten.
<p, fakt1, …, faktn> ist eine Liste und ein Element der Relation R mit
R = { x | es gibt fakt1, …, faktn so dass x = <p, fakt1, …, faktn> }
Woher kommen diese Entitäten?
p kann z.B. das Verb mag sein. Wenn die „variablen Fakten“ fakt1, …, faktn durch Namen wie „Peter“, „Susi“, „Monika“, „Hans“ und n durch 4 ersetzt werden, erhalten wir einen Satz. Inhaltlich gesprochen läuft eine Variable über Namen, oder anders gesagt über eine offene Menge von Personen. Wir haben eine Vorstellung, wie diese erörterte Personenmenge begrenzt ist.
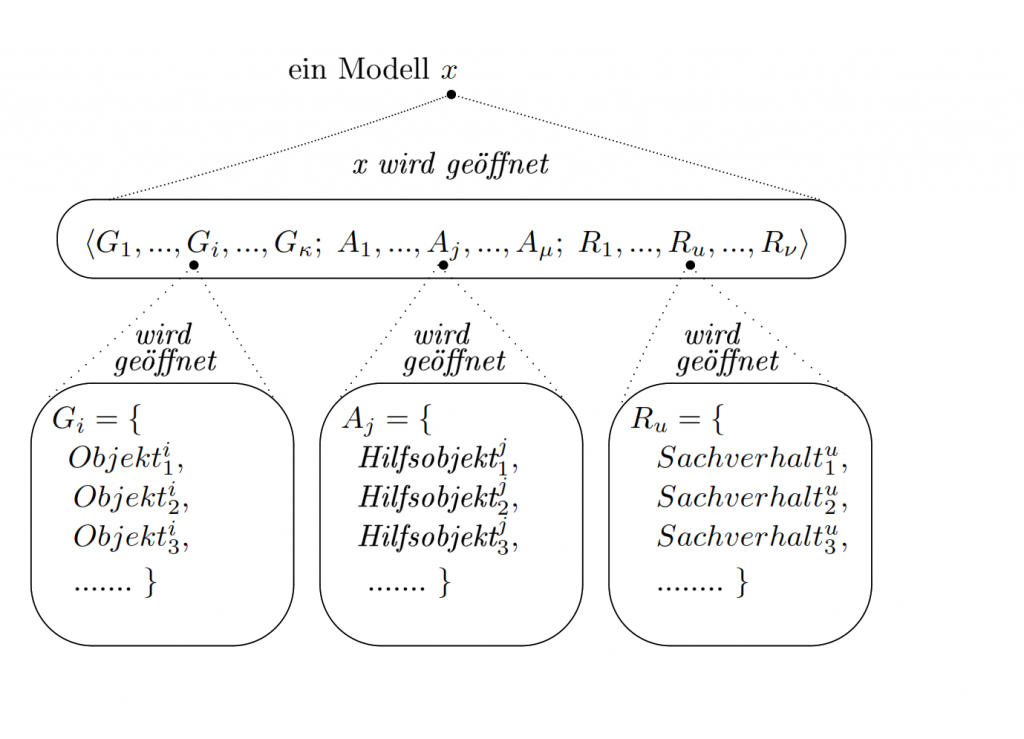
Ein Modell x hat also die Form x = <G1, …, Gk, A1, …, Am, R1, …, Rn>
wobei G1, …, Gk Mengen von Basismengen,
A1, …, Am Mengen von Hilfsbasismengen
und R1, …, Rn Relationen sind.
Der Begriff des Modells wird in der Logik genauer definiert. Wir beschränken uns hier darauf, den Modellbegriff durch Beispiele zu erläutern.
Ein Modell besteht aus Mengen und Elementen
Die Balancetheorie von Heider
- Kurze Beschreibung in Wikipedia.
- YouTube-Video.
- Detaillierte Beschreibung mit strukturalistischer Rekonstruktion und Modellierung in Prolog als PDF-Datei (© Dr. Klaus Manhart).
Abbildung von Modellen in Prolog – Erste Schritte
mag(peter, susi). /* Peter mag Susi */ mag(X, susi). /* Jeder mag Susi */ mag(peter, Y). /* Peter mag jeden */ mag(peter, Y), mag(Y, peter). /* Peter mag jeden und jeder mag Peter */ mag(peter, susi); mag(peter, monika). /* Peter mag Susi oder Peter mag Monika */ not(mag(peter, pizza)). /* Peter mag keine Pizza */ mag(peter, susi) :- mag(peter, monika). /* Peter mag Susi wenn Peter Monika mag */ /* X und Y sind Freunde wenn sie sich gegenseitig mögen */ freunde(X, Y) :- mag(X, Y), mag(Y, X). /* X hasst Y wenn X Y nicht mag*/ hasst(X, Y) :- not(mag(X, Y)), !. /* X und Y sind Feinde wenn sie sich gegenseitig nicht mögen */ feinde(X, Y) :- not(mag(X, Y)), not(mag(Y, X)), !.