2019 SoSe – Seminarstunde 06

Messung – fundamental und modellgeleitet

Einführung

Messung und Messmodell

Messung ist ein unverzichtbarer Bestandteil der Wissenschaft. Eine konkrete, wirklich statt­fin­dende Messung lässt sich immer durch ein «dazugehöriges» Modell, ein Messmodell dar­stellen. Messmodelle sind im Vergleich zu Modellen in drei Aspekten spezieller:

• Erstens be­schreibt ein Messmodell immer ein System, in das Wissenschaftler – in welcher Form auch immer – eingrei­fen. Das reale System wird durch Experimentatoren verändert. Das System kann marginal oder in Maßen verändert werden, es kann aber auch zerstört werden. Eine Raumsonde verändert den Planeten kaum, in einem Stoßexperiment wird in die Bahnen von Teilchen eingegriffen und bei einer chemischen Verpuffung wird eine Substanz zerstört.
• Zweitens enthält ein Messmodell die spezielle Bedingung der Eindeutigkeit. Ein hervorgehobener Bestandteil, wel­cher im Modell vorhanden sein muss, wird durch Hypothesen und durch einige andere gege­bene Teile des Modells, eindeutig bestimmt.
• Drittens enthält ein Messmodell immer – implizit oder explizit – eine oder mehrere Maßeinhei­ten, ohne die eine praktische Durchführung der Messung nicht möglich ist.

Fundamentale Messung

Messung der Größe einer Fläche

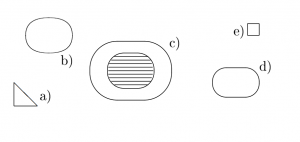
Flächen in verschiedenen Formen
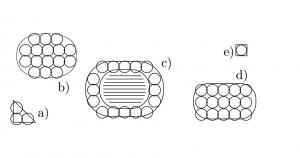
Mit Kreisen bedeckte Flächen		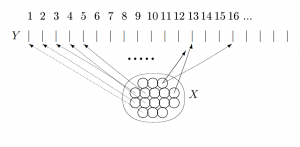Ein Zählvorgang
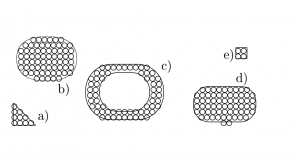
Mit kleinen Kreisen bedeckte Flächen

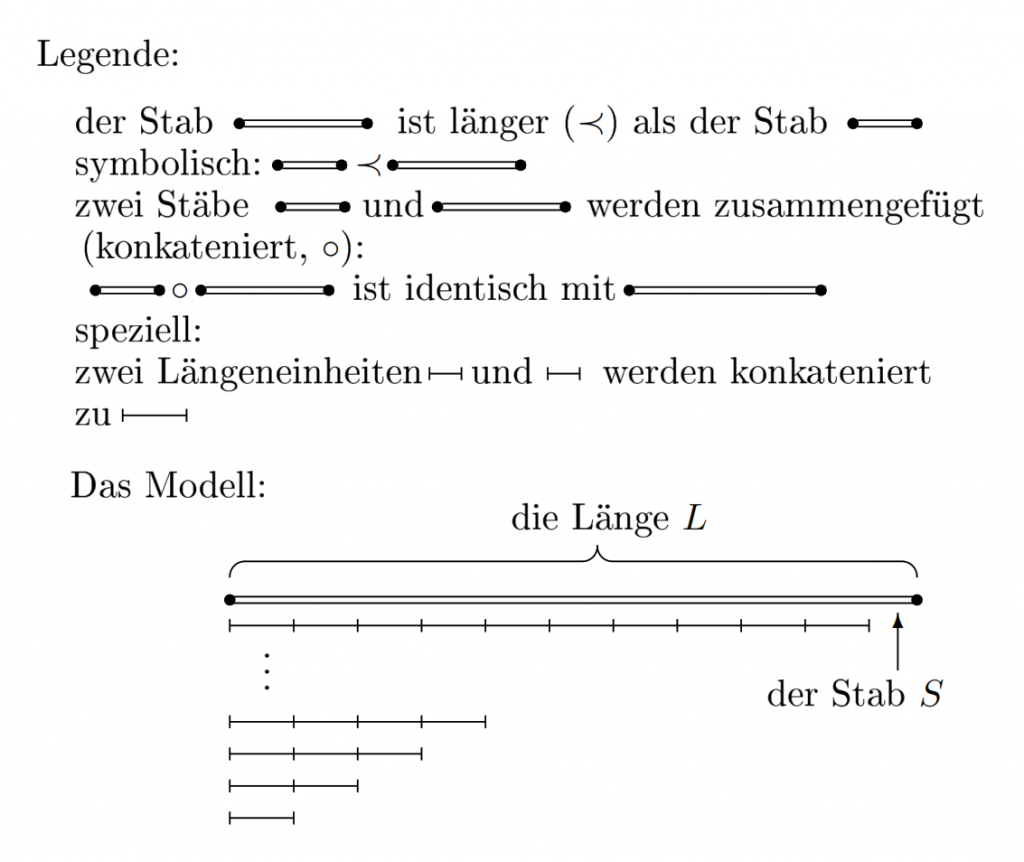
Abstandsmessung mit Metermaß

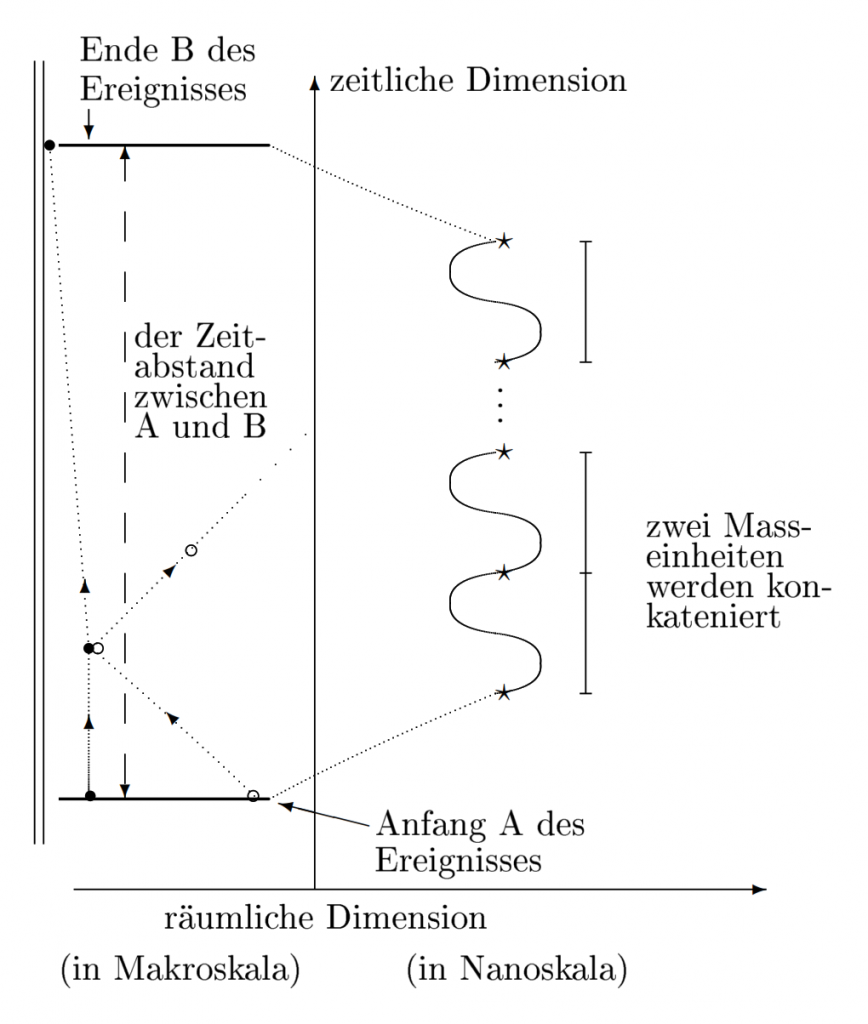
Zeitmessung eines Ereignisse mit Atomuhr

Die Theorie der fundamentalen Messung

Ein Modell der fundamentalen Messung enthält

• eine Menge G von Objekten,
• eine 2-stellige Relation < («echt kleiner») und
• eine 3-stellige Relation o (eine Funktion), die zwei Objekte x, y zu einem Objekt z «zusammenfügt» (konkateniert): o(x, y) = z.

Eine Hypothese für diese Modelle könnte z.B. sein:

• Für alle x, y und z aus G: wenn x < y, dann ist o(z, x) < o(z, y).

Modellgeleitete Bestimmung

Beispiel: Geometrische Triangulation

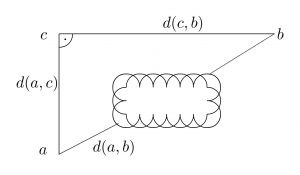
Messmodell

Ein Messmodell x hat dieselbe Form wie ein Modell. Zusätzlich werden bei ei­nem Messmodell zwei spezielle Teile des Modells hervorgehoben, die wir den vorausgesetz­ten Teil und den zu bestimmenden Teil des Messmodells nennen:

• Der vorausgesetzte Teil ent­hält Fak­ten, die implizit im Messmodell vorhanden sind und bei der Bestimmung verwendet werden müs­sen.
• Der zu bestimmende Teil des Messmodells soll dagegen erst bestimmt oder gemessen werden.

Gegenüber einem Modell erfüllt ein Messmodell darüber hinaus weitere Bedingungen:

• Erstens sind der vorausgesetzte und der zu bestimmende Teil des Messmodells disjunkt.
• Zweitens und zentral ist der zu bestimmende Teil eindeutig durch den vorausgesetz­ten Teil und durch die Hypothesen des Messmodells bestimmt.

Mit diesen allgemeinen For­mulie­run­gen können die vielen verschiedenen Messmethoden in einheitlicher Form be­schreiben werden.

Messmethode, Messtheorie, Messkette

Aus einem Messmodell lässt sich durch Abstraktion eine Menge von Messmodellen bilden, die als eine Messmethode bezeichnet wird. Eine Messmethode ist eine Menge von Modellen einer Theorie. Oft ist eine Messmethode eine echte Teilmenge einer Modellmenge einer The­orie. In solchen Fällen ist ein Messmodell ein Modell einer Theorie, aber die Messmethode beschreibt nur einen kleinen Teil der Gesamtmenge von Modellen der Theorie. Es gibt aber auch Mess­methoden, die keinen Teil einer «größeren» Theorie bilden. Eine solche Messme­thode kann als eine eigenständige Theorie angesehen werden. Wir nennen solche Messmethoden auch Mess­theorien.

Fügt man mehrere Messmodelle zusammen führt dies zu Messketten. Eine Messkette ist eine Folge x₁, …, x_n von Messmodellen, so dass der zu bestimmende Teil bt_i des Messmodells x_i in den vorausgesetzten Teil vt_i+1 des „nächsten” Messmodells x_i+1 aus der Messkette eingebettet wird.
Bei einem Messmodell aus einer Messkette wird der zu bestimmende Teil des Messmodells genommen und im darauf folgenden Messmodell der Kette im vorausgesetzten Teil verwen­det.