Autor: webmaster@theory-of-science.com

Theorienvergleich

Vier Dimensionen des Vergleichs

Wir unterscheiden vier Dimensionen des Vergleichs, die auch mit dem strukturalistischen Begriffsapparat beschrieben werden können. Diese vier Dimensionen bezeichnen wir wie folgt:

• Modellvergleich
• Vergleich der Faktensammlungen
• Vergleich der wissenschaftlichen Ansprüche
• Approximationsvergleich

Erste Dimension: Modellvergleich

Im Folgenden gehen wir von zwei Theorien T und T ⁰ aus, deren Komponenten wir hier auf folgende Weise abkürzen: T = 〈 STR, M, I, D, dist 〉 und T ⁰ = 〈 STR ⁰, M ⁰, I ⁰, D ⁰, dist ⁰ 〉. Ein Mo­dell x aus M hat die Form 〈 G₁, …, G_κ, A₁, …, A_μ, R₁, …, R_ν 〉 und ein Modell x ⁰ aus M ⁰ die Form 〈 G⁰₁, …, G⁰_κ⁰, A⁰₁, …, A⁰_μ⁰, R⁰₁, …, R⁰_ν⁰ 〉.

In der ersten Dimension, dem Modellvergleich, werden Modelle und die zugehörigen Hypo­the­sen der beiden Theorien verglichen.

Es werden zwei Begriffsfamilien erörtert, die mit den folgenden Termen bezeichnet werden:

• Einbettung
• Vermittlung

Modellvergleich durch Einbettung

Bei einer ersten Art von Einbettung wird ein Teil eines Modells x in einen Teil eines anderen Modells x ⁰ eingebettet. Im einfachsten Fall wird eine Grundmenge G_i von x in eine Grund­menge G⁰_j von x ⁰ eingebettet. Dazu müssen die Typisierungen der Modelle von M und M ⁰ bekannt sein. Genauer ist G_i die i-te Grundmenge von x, G⁰_j die j-te Grundmenge von x ⁰ und G_i eine echte oder unechte Teilmenge von G⁰_j, das heißt G_i ⊂ G⁰_j oder G_i ⊆ G⁰_j. Oft sind die Grund­mengen in beiden Modellen auf derselben Stelle aufgeführt: i = j ⁰. Auf dieselbe Weise lassen sich Hilfsbasismengen aus einem Modell x in Hilfsbasismengen aus einem Modell x ⁰ einbetten.

Bei einer zweiten Art von Einbettung wird eine Relation R_i aus einem Modell x von T in eine Relation R⁰_j aus einem Modell x ⁰ von T ⁰ eingebettet. In diesen Fällen müssen die Typisierun­gen τ_i und τ⁰_j der Relationen und ihre Ordnungsindizes genau angegeben werden. Genauer wird diese Einbettung wie folgt formuliert: es gibt Typisierungen τ_i und τ⁰_j , so dass es für jedes Modell x ∈ M und für jede Relation R_i der Typisierung τ_i aus x ein Modell x ⁰ ∈ M ⁰ und eine Relation R⁰_j der Typisierung τ⁰_j aus x ⁰ gibt, so dass R_i eine echte Teilmenge von R⁰_j ist, kurz: R_i ⊂ R⁰_j .

Einbettung von Komponenten zweier Modelle

Modelle mit einer zusätzlichen Relation R^*

Modellvergleich durch Vermittlung

Bei einer Theorienvermittlung stehen die Komponenten zweier Modelle nicht in einem Teilmengenverhältnis. Zwei Kompo­nenten müssen auf eine andere Art und Weise verglichen werden; sie stehen nur noch vermit­telt in Beziehung. Die Teilmengenbeziehung wird so verallgemeinert, dass eine Komponente auf eine andere Komponente abgebildet wird. Mengentheoretisch lässt sich dies durch den Funktionsbegriff realisieren. Eine Funktion Φ wird als «Vermittler» für die Beziehung beider Kompo­nenten verwendet.

Eine erste Art von Theorienvermittlung wird als Äquivalenz von Theorien T und T ^‘ bezeich­net. Es wird auch die Bezeichnung äquivalente Darstellung verwendet. Auf Modellebene wird eine bijektive Abbildung φ zwischen den Modellmengen M und M ^‘ eingeführt. Die in­verse Abbil­dung der Funktion φ wird zum Beispiel so geschrieben: φ^. Jedes Modell x aus M wird eindeutig in ein Modell x ‘ abgebildet: x ‘ = φ ( x ) – und umgekehrt wird jedes Modell x ^‘ aus M ^‘ in ein Modell x abgebildet: x = φ ^ ( x ‘ ).

Auf der Sprachebene wird Äquivalenz durch Ableitung ausgedrückt. Die Hypothesen H von T werden durch die Hypothesen H ^‘ von T ^‘ abgeleitet – und umgekehrt. Solche Äquivalenzen findet man bis jetzt fast nur in der Mathematik und der Physik.

Zwei äquivalente Darstellungen eines Raumes

Bei einer zweiten Art von Theorienvermittlung werden nur Teile von Komponenten in Bezie­hung gesetzt. In der obigen Abbildung «Einbettung von Komponenten zweier Modelle» enthält der Durchschnitt der Relationen R_i und R^*_j viele Ele­mente. Bei einer Theorienvermittlung kann ein solcher Durchschnitt hingegen leer sein. So kann es zum Beispiel sein, dass zwei Grundmengen kein einziges Element gemeinsam haben. Durch eine Funktion werden zwei disjunkte Relationen oder Grundmengen aufeinander abge­bildet. Bei der hier erörterten Situation können wir in der obigen Abbildung die Relationen R_i und R^*_j disjunkt werden lassen und eine Funktion φ dazwischenschalten, so dass die Elemente (Er­eig­nisse) von R_i auf solche von R^*_j abgebildet werden.

Eine letzte Art von Vermittlung entsteht durch Verknüpfung. Die Zuordnung geschieht nicht durch eine Funktion allein. Ein Argument der Funktion η wird durch eine Gleichung oder durch eine andere abstrakte Beziehung in einen Funktionswert von η transformiert.

Theorienvermittlung durch Verknüpfung

Zweite Dimension: Vergleich der Faktensammlungen

In der zweiten Dimension wird mit dem Vergleich der Faktensammlungen die Vermittlung von der Modellebene auf die Ebene der Faktensammlungen heruntergezogen. Bei einer Vermitt­lung zwischen Faktensammlungen geht es im Wesentlichen um «kleine» Mengen von realen, ele­mentaren Ereignissen. Bei einer Vermittlung zwischen Modellen geht es dagegen meist um unendlich viele Elemente, die durch Terme mit Variablen beschrieben werden. Auf Ebene der Faktensammlungen werden also Fakten in den Vordergrund gerückt, während es auf der Modellebene um Hypothesen geht.

Eine Faktensammlung besteht aus Listen von Mengen von elementaren Ereignissen und Sach­verhalten. Für eine solche Menge liegt aber kein allgemein formulierter Satz vor. Meist wird eine Komponente einer Faktensammlung wieder als eine Liste von Ereignissen, Sach­verhalten oder Objekten geführt. Jedes real untersuchte Ereignis erhält eine Bezeichnung, die das Ereignis identifiziert. Dagegen geht es in einem Modell um allgemeine, variabel ausge­drückte Ereignisse oder Sachverhalte. Der Zusammenhalt von Ereignissen entsteht erst auf der Modellebene, wenn Hypothesen für das Modell beschrieben werden.

Gemeinsame Fakten aus Faktensammlungen

Dritte Dimension: Vergleich der wissenschaftlichen Ansprüche

Vierte Dimension: Approximationsvergleich

In der vierten Dimension werden die Approximationsapparate zweier Theorien verglichen.

Zwei Theorien können die gleiche Approximationsmethode verwenden. In diesem Fall lässt sich der Vergleich auf Abstandskonstanten zurückführen. Diese Konstanten hängen von der Anzahl der Faktensammlungen, der jewei­ligen Größe einzelner Faktensammlungen und von der Struktur der Modelle der Theorien ab. Wenn es in der Theorie T beispielsweise um wenige Faktensammlungen geht, kann keine Faktensammlung vernachlässigt werden. Eine Umgebungskonstante k_D für die Menge D der Fak­tensammlungen kann in diesem Fall nicht variiert werden. Nur die Umgebungskonstante k_x, die von der Anzahl der Elemente in den Grundmengen der Modelle x abhängt, lässt sich variieren. Wenn eine neue, «bessere» Theorie T ⁰ gefunden wird, müssen die Konstanten 〈 k_D, k_x 〉 mit den entsprechenden Konstanten 〈 k⁰_D⁰, k⁰_x⁰ 〉 der Theorie T ⁰ verglichen werden. Die Gewichtung der Konstanten und die Struktur der Modelle kommen ins Spiel. All dies führt in die Statistik, die für die Wissenschaftstheorie inzwischen unerlässlich geworden ist.

Entstehung und Änderung von Theorien

Entstehung von Theorien

Wie kann eine neue Theorie entstehen?

• Eine Person muss ein Ereignis wahrnehmen, das ihr bis jetzt noch unbekannt war.
• Der Beobachter muss mit anderen Personen sprechen können.
• Das Ereignis muss in der verwendeten Sprache formulierbar sein, so dass es von anderen Ereignissen, die im wahrgenommenen Umfeld des Ereignisses liegen, unterschieden werden kann.
• Das in Frage stehende Ereignis muss unerwartet, anders oder neu erscheinen.
• Es sollte nicht ohne weiteres der Fall sein, dass die betreffenden Personen das Ereignis durch lebensweltliche, praktische Zusammenhänge mit der Umgebung verbinden können (isoliertes Problem).
• Die Person muss Interesse und eine Idee haben. Sie entwirft ein neues Modell, welches das Ereignis darstellt, es von anderen Ereignisse abgrenzt und mit anderen Ereignissen in Verbindung bringt. Die Person teilt dieses neue Modell Anderen mit.
• Es muss der Fall eintreten, dass einige Personen diese neue Idee positiv aufnehmen.

Der Prozess

• Eine Person nimmt ein für sie nicht erklärbares System – ein Ereignis, ein Phänomen – wahr.
• Sie beginnt das System begrifflich zu analysieren. Sie verwendet dazu einige Worte, die sie bereits kennt und beschreibt einige Aspekte des Systems. Teile, Ob­jekte, Sachverhalte, Ereignisse des Systems und Prozesse, die innerhalb des Systems liegen und andere, die von und zur Umgebung führen, werden identifiziert und mit Bezeichnungen verse­hen.
• Bei Prozessen werden möglichst allgemeine Ausdrücke verwendet, vor allem wenn Pro­zesse oder Teile davon wiederholt wahrgenommen werden. Durch allgemeine Ausdrücke wird es möglich, Hypothesen zu bilden.
• In einem ersten Versuch wird ein Modell entworfen. Be­griffe für Grundmengen und Relationen werden gebildet, bestimmt, verwendet, «fest­gestellt». Mit diesen und eventuell mit bekannten, mathematischen Begriffen werden erste Hy­pothesen formuliert.
• Gleichzeitig wird überlegt, ob es Methoden gibt, die bestimmte Teile, wie Objekte oder Sach­verhalte, genauer bestimmen können. Zusätzlich werden neue Methoden entworfen, mit denen man eventuell einige Prozesse in den Griff bekommen kann.
• Auf diese Weise werden verschiedene Fakten produziert mit denen neue Hypothesen über­prüft werden können. In einem ersten Anlauf passen die Fakten eventuell nicht zu den neu erdachten Hypothesen, so dass an den Hypothesen gefeilt werden muss.
• Spätestens nach dem diese Aktivitäten zu einem ersten guten Ende gekommen sind, muss die Person ihr neues Wissen mit anderen teilen. Dies kann positiv ausgehen, wenn Andere die In­formationen interessant und originell finden. Es kann aber auch passieren, dass der Erfinder keine Rückmeldung bekommt, obwohl er seine Resultate veröffentlicht hat. Das menschliche Umfeld kann sich neutral, interessiert, aber auch feindselig verhalten. Die Erfinder können sich in einer mehr kooperativen oder in einer ausgeprägten Wettbewerbssituation befinden.
• Wenn ein erstes Modell existiert, andere Personen dieses Modell ebenfalls akzeptieren und wenn alle diese Personen das untersuchte Systeme oder mehrere davon tatsächlich kennenge­lernt haben und interessant finden, hat sich eine neue Theorie gebildet. Ein Modell, und damit formal eine ganze Menge möglicher Modelle, ein erstes intendiertes System und eine neu ent­standene Gruppe von Forschern bilden eine neue Theorie.
• In einem nächsten Schritt wird der Anwendungsbereich der verwendeten Bestimmungsmethoden erweitert. Dies geschieht auf unterschiedlichen Weisen. Zum Beispiel kann das intendierte System in Wirklichkeit größer sein; am An­fang wurde aber nur ein zentraler Teil des Systems untersucht. In einem weiteren Schritt wird dann die Untersuchung auf weitere Teile des Systems ausgeweitet. In einem anderen Erweite­rungs­verfahren kann das Modell auf andere, ähnliche Systeme angewandt werden. Solche Möglich­keiten werden durch Kommunikation weiter vervielfältigt. Andere Interessenten oder Wettbe­werber treten auf den Plan. Die Theorie wächst. Neue intendierte Systeme, Fakten­sammlungen und weitere spezielle Hypothesen kommen hinzu.

Beispiel: Elektrizitätstheorie von Ohm

Als Beispiel für eine Theorie, die mehrere Anläufe brauchte um sich durchzusetzen, gilt die Elektrizitätstheorie von Ohm:

• Im siebzehnten Jahrhundert war es Mode ein spezielles, paradigmatisches Phänomen zu untersuchen, nämlich das Zucken von to­ten Froschschenkeln und den damit verbundenen elektrischen Schlägen.
• In der Periode zwischen 1650 und 1830 wurden verschiedene elektrische Phänomene ent­deckt, die durch mehrere Arten von teilweise inhomogenen Formulierungen beschrieben wur­den.
• Die intendierten Systeme der Ohmschen Theorie lassen sich in einer üblichen Formulierung über Elektrizität etwa so ausdrücken. Ein intendiertes System besteht aus einer Stromquelle, einer Batterie (mit zwei Polen + und -), aus einem elektrischen Leiter, aus einem Kabel, dessen Enden mit den beiden Polen «kurzgeschlossen» werden können und aus einer fast strom­undurchlässigen Substanz. Der Leiter ist durch die Substanz isoliert; die Elektrizität bleibt im Stromkreis.
• Von Ohm wurde hierzu ein Modell entworfen. Die dazugehörige Hypothese wird heute meist so formuliert: I = U / R. I ist die Stromstärke, U die Spannung und R der Widerstand – relativ zu einem bestimmten Stromkreis. Ein Stromkreis ist anders gesagt ein intendiertes System für die Ohmsche Theorie und wird durch diese drei Größen beschrieben.

Wichtige Komponenten der Entstehung von Theorien

Änderung einer Theorie

Theorien werden verändert durch:

• Änderung der Grundmengen aus den Faktensammlungen der Theorie
• Änderung der Relationen aus einer Faktensammlung
• Änderung von Definitionen zu den Hypothesen
• Änderung von Verknüpfungen

Veränderung einer Menge

Einführung

Die Veränderung einer Menge lässt sich in zwei Schritten erklären.

Erstens benötigen wir für eine Veränderung ein Paar 〈 X, Y 〉 von Mengen, so dass sich die erste Menge X so verändert hat, dass sie zu einer anderen Menge Y geworden ist.

Zweitens muss der Ausdruck X verän­dert sich zu Y genauer bestimmt werden. Dazu gehen wir von zwei gegebenen Mengen X und Y aus. Der Ausdruck X verändert sich zu Y erfüllt per Definition zwei Bedingungen:

• Die Mengen X und Y sind verschieden ( X ≠ Y ).
• Die meisten Elemente von X gehören auch zu Y und die meisten Elemente von Y gehören auch zu X.

Beispiele

• In der Gravitationstheorie wurde im Jahre 1930 ein neuer Planet entdeckt, der den Namen Pluto bekam. Die kleinen und im Sonnensystem weit außen liegenden Planeten wurden erst spät entdeckt da geeignete Messinstrumente erst erfun­den werden mussten. Die Himmelskörper selbst haben sich nicht geändert haben, es fand eine Veränderung auf der Ebene der Theorie statt. Das «Objekt» Pluto bekam nach einiger Zeit einen Namen und dieser Name wurde in die Liste der Planeten aufgenommen. Im Jahre 2006 wurde Pluto der Planetenstatus von der International Astronomical Union (IAU) wieder aberkannt. Die Menge der Planeten hängt daher nicht nur von den realen Verhältnissen ab, sondern auch von den Aktivitäten der Wissenschaftlergrup­pen, welche die Theorie untersuchen.
• In der Zellbiologie wird in einem Laborexperiment eine Zellkultur angelegt und mit einem Namen versehen. Eine Faktensammlung der Theorie enthält eine Menge von Basisereignissen, in diesem Fall Zellkulturen. Eine neue Zellkultur wird der Menge von schon untersuchten Zellkulturen hinzugefügt. Auch die Zellkultur hat im Prinzip die Form eines Ereignisses: die Zellkultur wächst. Auf der Sprachebene wird eine Liste von Namen von Zellkulturen geführt. Auf der Ebene der Mengen wird die neue Zellkultur zur Menge der Zell­kulturen hinzugefügt. Die Menge der Basisereignisse aus diesen Faktensamm­lungen hat sich damit verändert.
• In der Ökonomie werden Oligopole untersucht, das heißt Märkte, in denen es nur wenige oder nur zwei Anbieter gibt. In wirklich untersuchten Anwendungen wird zum Beispiel ein neues Unternehmen gegründet. Dieses neue «Objekt» wird einer Menge von Basisereignissen der zugehörigen Faktensammlungen hinzugefügt. Die Theorie der Oli­go­pole hat eine kleine Veränderung erfahren.

Formale Darstellung

In diesen Beispielen ist in allgemeiner Formulierung eine Grundmenge G_i^z zu einer anderen Grundmenge G_i^z+1 geworden. G_i^z hat sich zu G_i^z+1 verändert Diese Veränderung lässt sich auf zwei Grundveränderungen zurückführen:

• Erstens kann G_i^z+1 aus G_i^z entstehen, wenn aus der Sicht von G_i^z ein neues Element e zu G_i^z hinzugefügt wird: G_i^z+1 = G_i^z ∪ {e}.
• Zweitens kann ein Element aus G_i^z entfernt werden: G_i^z+1 = G_i^z ∖ {e}.

Aus diesen beiden Grundänderungen lässt sich zum Beispiel eine Ersetzung definieren. Ein Element e wird aus G_i^z entfernt und dann wird der so entstehenden Menge ein neues Element e* hinzugefügt.

Wird eine Element entfernt, so muss darauf geachtet werden, dass auch Teile der Relationen aus der Faktensammlung entfernt werden. Das Faktum d kann zum Beispiel ein Sachverhalt aus der Relation R_j^z zum Zeitpunkt z sein und eine konkrete Beziehung zu anderen Elementen haben. In solchen Fällen muss diese Beziehung aus der Relation R_j^z ebenfalls entfernt werden, da in einer Faktensammlung nur wirkliche Beziehungen geführt werden.

Veränderung von Komponenten eines Modells

Hinzufügen einer Definition zu den Hypothesen

Bei einer weiteren Veränderungsart wird eine Definition zu den Hypothesen der Theorie hin­zugefügt. Zur Theorie kommt ein neuer Begriff hinzu, welcher einerseits auf die schon verwendeten Grundbegriffe zurückgeführt wird, der aber andererseits bei der Beschreibung einer Hypo­these so viel Formulierungsaufwand einspart, dass dieser eigentlich redundante Begriff trotz­dem explizit als Teil der Theorienbeschreibung gesehen wird.

Im Beispiel der Partikelmechanik wird im Modell 〈 P, T, ℜ, ℜ³ ,s ,m , f  〉 die zentrale Hypothese  f = m × a verwendet (Kraft = Masse x Beschleunigung), in der die Ortsfunktion s nicht erscheint. Der Begriff a der Beschleunigung wird in dieser Theo­rie explizit aus der Ortsfunktion definiert. Die Definition hat die Form F( P, ℜ, ℜ³, s, a ) eines satzartigen Terms. Inhaltlich ist P die Grundmenge der Partikel. Die Menge der Zeitpunkte des Modells sind mit dem mathematischen Raum ℜ gleichgesetzt. ℜ und ℜ³ sind Hilfs­basismengen, welche die Zeit und den Raum darstellen. In dieser Definition wird die Funktion s zweimal differenziert. Aus der Ortsfunktion s wird die Geschwindigkeitsfunktion v. Die Funktion v wird explizit aus s definiert: v = Ds oder genauer: für alle p und z gilt: v( p, z ) = Ds( p, z ). Im zweiten Schritt wird die Geschwin­digkeitsfunktion v differenziert. So entsteht die explizit definierte Beschleuni­gungsfunktion a:
a = Dv = D²s und für alle p und z gilt: a( p, z ) = D²s( p, z ).

Hinzufügen einer neuen Verknüpfung

Als weitere Änderung wird bei einem Modell eine neue Verknüpfung (engl. Link) hin­zu­gefügt. Im einfachsten Fall ver­knüpft ein Begriff aus der gegebenen Theorie T einen anderen Begriff aus einer weiteren The­orie T^*. Auch die Verknüpfungsrelation hängt von den Modellen ab. Eine Relation aus einem Modell der Theorie T wird mit einer Relation eines Modells der Theorie T^* verknüpft.

Verknüpfung lässt sich genauer wie folgt definieren. Dabei sind zwei Theorien T und T^* mit ihren Modellen M und M^* und den dazugehörigen Strukturen 〈 κ, μ, ν, τ₁, …, τ_ν 〉 und 〈 κ^*, μ^*, ν^*, τ^*₁ ,…, τ^*_ν^* 〉 gegeben. Eine Verknüpfungshypothese hat die Form V( R, R^*, x, x^*, t_i, t^*_j ).

Dabei ist V eine Formel, x und x^* sind Modelle aus M und M^* und τ_i und τ^*_j sind die Typisie­rungen der Relationen R und R^*. R muss die i-te Relation von x und R^* die j-te Relation von x^* sein und die Formel V( … ) muss den obigen Term erfüllen. Ein Paar solcher Relationen R und R^* stellt eine konkrete Verknüpfung von Relationen (relativ zu gegebenen Theorien) dar. Wir können daher auch von einer Verknüpfung eines Begriffs von T mit einem Begriff von T^* sprechen.

Relativ zu i und j ist R mit R* verknüpft genau dann wenn es Modelle x ∈ M und x^* ∈ M^* und Typisierungen τ_i und τ^*_j gibt, so dass gilt:

• R ist durch τ_i und R^* durch τ^*_j typisiert
• R ist die i-te Relation von x und R^* ist die j-te Relation von x^*
• R und R^* erfüllen die Verknüpfungshypothese V( R, R^*, x, x^*, τ_i, τ^*_j ).

Struktur und Invarianz

Struktur eines Modells und einer Modellklasse

Struktur der Modelle einer Theorie

Die Struktur der Modelle einer Theorie enthält zwei Teile, nämlich erstens drei natürliche Zah­len κ, μ und ν und zweitens für jede Zahl i ≤ ν eine Typisierung τ_i. κ ist die Anzahl der Grund­mengen, μ die Anzahl der Hilfsbasismengen und ν die Anzahl der Relationen aus Mo­dellen einer Theorie. Dabei sind κ und ν positive Zahlen, während μ auch Null sein kann.

Eine Typisierung τ_i ist eine kodierte Regel, welche angibt, wie Relationen der Art Nummer i aus Grundmengen und aus Hilfsbasismengen des Modells zusammengesetzt werden. Der Be­griff der Typisierung nimmt in der Wissenschaftstheorie einen zentralen Platz ein.

Eine Theorie T hat immer auch eine Struktur STR. Die Struktur STR wird durch die Zahlen κ, μ, ν und die ν Typisierungen τ₁, …, τ_ν beschrieben: STR = 〈 κ, μ, ν, τ₁, …, τ_ν 〉.

Der Begriff der Struktur bezieht sich in erster Linie auf die Theorie, erst in zweiter Linie auf bestimmte Modelle. Eine Typisierung τ_i in einer Theorie gilt für alle Relationen, die als ( κ + μ + i )-te Komponente der Modelle zu finden sind.

Typisierte Potenzmenge

Das Verfahren der Typisierung führt zu einer großen Menge (der Potenzmenge) von Möglichkeiten, es wird aber kein bestimmtes Element aus diesen Möglichkeiten ausgewählt. Die Auswahl eines bestimmten Elements aus der typisierten Potenzmenge, bleibt an die­ser Stelle völlig offen. Es hätte auch eine andere Relation aus der Potenzmenge entnom­men werden können.

Somit kann man sagen, dass sich aus einem Modell dessen Struktur eindeutig ergibt, aber umgekehrt aus einer Struktur nicht das Modell, welches über diese Struktur verfügt. Ausgehend von gegebenen Grundmengen und Typisierungen legt die Struktur nur fest, in welcher Potenzmenge die Relation R_i liegt, aber nicht wie sie im Detail aussieht.

Mehr lässt sich nur sagen, wenn die Hypothesen für das Modell genauer spezifiziert werden. Fest steht, dass eine gegebene Modellklasse eine eindeutig bestimmte Struktur hat. Alle Modelle der Klasse haben dieselbe Struktur.

Kartesisches Produkt und Potenzmenge

Anwendungsbereiche für den Strukturbegriff

Der so beschriebene Begriff der Struktur wird in der Wissenschaftstheorie für drei verschie­dene Bereiche von Untersuchungen eingesetzt:

• In einem ersten Bereich werden verschiedene Transformationen von Modellen untersucht. Ein bestimmter Aspekt, ein Teil des Modells, bleibt bei einer Transformation gleich; eine Eigen­schaft eines Modells bleibt invariant.
• In einem zweiten Anwendungsbereich der Wissenschaftstheorie wird der Strukturbegriff ein­gesetzt, wenn eine Struktur in mehreren Disziplinen verwendet wird. Es gibt einige Fälle, in denen zwei Modelle aus verschiedenen Theorien dieselbe Struktur haben. Es gibt auch Fälle, in denen zwei Modelle beider Theorien zwar nicht die gleiche Struktur haben, aber Teilmo­delle aus beiden Theorien dieselbe (Teil-) Struktur besitzen.
• Eine weitere Anwendung des Strukturbegriffs betrifft die Übertragung der Struktur von Mo­del­len und der Modellklassen auf die gesamte Theorie. Dieser Punkt ist wissenschaftstheore­tisch interessant, weil er verschiedene Unterscheidungen und Klassifizierungen ermöglicht.

Wissenschaftstheorie und Wahrscheinlichkeit

Statistische Bestimmung

Einführung

Die bisher erörterten Bestimmungsmethoden kommen ohne den Begriff der Wahrscheinlich­keit aus. Es gibt aber viele Bereiche, in denen diese Bestimmungsmethoden nicht funktionie­ren:

• Es kann zu wenig Fakten geben, um eine Bestimmung durch­zuführen oder die Hypothesen können zu vage formuliert sein.
• Es kann aber auch sein, dass eine sichere Vorhersage grundsätzlich nicht möglich ist. Dies liegt an der Welt der Ereignisse. Eine Ursache – ein Ereignis – kann mehrere, sich ausschließende Wirkungen haben. Nur eine Wirkung tritt ein, aber andere Wirkungen hätten ebenfalls real eintreten können. Diese Wir­kungen können nur als wahrscheinlich angesehen werden, so lange keine davon tatsächlich eingetreten ist. Bei der Formulierung, dass etwas eine bestimmte Wahrscheinlichkeit hat, muss erstens einigerma­ßen klar sein, welcher Entität die Wahrscheinlichkeit zugeschrieben wird und zweitens in wel­chem Bereich die Entität liegt.

Statistische Grundbegriffe

Um eine be­stimmte Wahrscheinlichkeit zu untersuchen, wird ein satzartiger Ausdruck mit einer Variab­len verwendet, der eine Menge von Ereignissen bezeichnet. Wenn die Variable durch einen «Namen» ersetzt wird, erhalten wir einen variablenfreien Ausdruck, welcher ein «echtes» Er­eignis be­schreibt. In der Wahrscheinlichkeitstheorie bilden Ereignisse und Ereignismengen die Grunde­lemente, aus denen die Modelle der Wahrscheinlichkeitstheorie konstruiert werden können. Diese Modelle werden Wahrscheinlichkeitsräume oder kurz W-Räume genannt.

Inzwischen gibt es zwei verschiedene Formulierungen der Wahrscheinlichkeitstheorie. Im «klassischen» Originalansatz, den wir hier verwenden, wird einer Entität, ei­nem so genannten Zufallsereignis (random event), eine Wahrscheinlichkeit zu­gesprochen. Ein Zufallsereignis ist mengentheoretisch gesprochen eine Menge von konkre­ten, realen oder nur möglichen Ereignissen. All die Ereignisse aus einer solchen Menge sind sich ähnlich; sie sind durch dieselbe Formel beschrieben. Diese Ereignisse unterscheiden sich bei einer Beschreibung nur in einer einzigen Eigenschaft. Auf Sprachebene kann ein Ereignis durch einen deutschen, grammatisch korrekten Satz ausgedrückt werden. Dagegen wird ein Zufalls­ereignis durch eine Formel beschrieben, die eine freie Variable enthält.

Die Elemente aus einem Zufallsereignis nennen wir Elementarereignisse. Um hier drohenden Mehrdeutigkeiten zuvorzukommen, vermeiden wir in wahrscheinlichkeitsthe­o­retischen Kontexten das Wort «Ereignis» und verwenden in solchen Zusammenhängen im­mer das Wort «Elementarereignis». Ein «normales» Ereignis wird also bei der Diskussion von Wahrscheinlichkeiten ein Elementarereignis und ein Zu­fallsereig­nis wird als eine Menge von Elementarereignissen betrachtet.

Im Allgemeinen wird eine Funktion eingeführt, die jedem Elementarereignis eine reelle Zahl zuordnet. Diese Funktion spielt in der Wahrscheinlichkeitstheorie eine Schlüsselrolle; sie wird Zufallsvariable genannt. Dass es sich um eine Variable handelt, sieht man daran, dass sich die Elementarereignisse in einer Menge von möglichen, zufällig stattfindenden Ereignis­sen befin­den. So lange keines der erwarteten Elementarereignisse stattgefunden hat, werden sie variabel behandelt und untersucht. Auf der Beschreibungsebene wird eine Variable verwendet, die über die verschiedenen möglichen Elementarereignisse läuft.

Beispiel: Demokratische Wahl des Präsidenten der USA

Randbedingungen:

• Bei dieser Wahl gibt es meist nur zwei Kandidaten aus den beiden großen Politiklagern, die wir A und B nennen.
• Ein Wähler hat genau eine Stimme und die Stimmab­gabe ist geheim.
• Aus Einfachheitsgründen wird das für Nicht-US Bürger etwas merkwürdige System der Wahlmänner unberücksichtigt gelassen und zusätzlich gefordert, dass jeder Wähler seine Stimme abgeben muss und dass er genau einen der beiden Kandidaten wählen muss.

Bei einer solchen Wahl gibt es eine feste Anzahl n von Wählern. Bei einer Stimmabgabe gibt es also nur zwei Möglichkeiten: ein Wähler w wählt Kandidat A oder w wählt Kandidat B. Die Wahrscheinlichkeitstheorie lässt sich dabei auf verschiedene Weise ins Spiel bringen. Dies hängt unter anderem von den Ereignisarten ab, die man bei einer Beschreibung einer Wahl ver­wendet. Man könnte zum Beispiel fragen:

(a)     Wählen k Wähler den Kandidaten A?

(b)     Gewinnt A mit einer Mehrheit von Wahlstimmen?

(c)     Stimmt Wähler w für Kandidat A?

Mögliche Wahlresultate und eine Stichprobe

Mögliche Wahlresultate und Elementarereignisse

Verteilung von Elementarereignissen

Gleichverteilte, zufällige, binomiale und stetige Verteilungen

Messung – fundamental und modellgeleitet

Einführung

Messung und Messmodell

Messung ist ein unverzichtbarer Bestandteil der Wissenschaft. Eine konkrete, wirklich statt­fin­dende Messung lässt sich immer durch ein «dazugehöriges» Modell, ein Messmodell dar­stellen. Messmodelle sind im Vergleich zu Modellen in drei Aspekten spezieller:

• Erstens be­schreibt ein Messmodell immer ein System, in das Wissenschaftler – in welcher Form auch immer – eingrei­fen. Das reale System wird durch Experimentatoren verändert. Das System kann marginal oder in Maßen verändert werden, es kann aber auch zerstört werden. Eine Raumsonde verändert den Planeten kaum, in einem Stoßexperiment wird in die Bahnen von Teilchen eingegriffen und bei einer chemischen Verpuffung wird eine Substanz zerstört.
• Zweitens enthält ein Messmodell die spezielle Bedingung der Eindeutigkeit. Ein hervorgehobener Bestandteil, wel­cher im Modell vorhanden sein muss, wird durch Hypothesen und durch einige andere gege­bene Teile des Modells, eindeutig bestimmt.
• Drittens enthält ein Messmodell immer – implizit oder explizit – eine oder mehrere Maßeinhei­ten, ohne die eine praktische Durchführung der Messung nicht möglich ist.

Fundamentale Messung

Messung der Größe einer Fläche

Flächen in verschiedenen Formen
Mit Kreisen bedeckte Flächen		Ein Zählvorgang
Mit kleinen Kreisen bedeckte Flächen

Abstandsmessung mit Metermaß

Zeitmessung eines Ereignisse mit Atomuhr

Die Theorie der fundamentalen Messung

Ein Modell der fundamentalen Messung enthält

• eine Menge G von Objekten,
• eine 2-stellige Relation < («echt kleiner») und
• eine 3-stellige Relation o (eine Funktion), die zwei Objekte x, y zu einem Objekt z «zusammenfügt» (konkateniert): o(x, y) = z.

Eine Hypothese für diese Modelle könnte z.B. sein:

• Für alle x, y und z aus G: wenn x < y, dann ist o(z, x) < o(z, y).

Modellgeleitete Bestimmung

Beispiel: Geometrische Triangulation

Messmodell

Ein Messmodell x hat dieselbe Form wie ein Modell. Zusätzlich werden bei ei­nem Messmodell zwei spezielle Teile des Modells hervorgehoben, die wir den vorausgesetz­ten Teil und den zu bestimmenden Teil des Messmodells nennen:

• Der vorausgesetzte Teil ent­hält Fak­ten, die implizit im Messmodell vorhanden sind und bei der Bestimmung verwendet werden müs­sen.
• Der zu bestimmende Teil des Messmodells soll dagegen erst bestimmt oder gemessen werden.

Gegenüber einem Modell erfüllt ein Messmodell darüber hinaus weitere Bedingungen:

• Erstens sind der vorausgesetzte und der zu bestimmende Teil des Messmodells disjunkt.
• Zweitens und zentral ist der zu bestimmende Teil eindeutig durch den vorausgesetz­ten Teil und durch die Hypothesen des Messmodells bestimmt.

Mit diesen allgemeinen For­mulie­run­gen können die vielen verschiedenen Messmethoden in einheitlicher Form be­schreiben werden.

Messmethode, Messtheorie, Messkette

Aus einem Messmodell lässt sich durch Abstraktion eine Menge von Messmodellen bilden, die als eine Messmethode bezeichnet wird. Eine Messmethode ist eine Menge von Modellen einer Theorie. Oft ist eine Messmethode eine echte Teilmenge einer Modellmenge einer The­orie. In solchen Fällen ist ein Messmodell ein Modell einer Theorie, aber die Messmethode beschreibt nur einen kleinen Teil der Gesamtmenge von Modellen der Theorie. Es gibt aber auch Mess­methoden, die keinen Teil einer «größeren» Theorie bilden. Eine solche Messme­thode kann als eine eigenständige Theorie angesehen werden. Wir nennen solche Messmethoden auch Mess­theorien.

Fügt man mehrere Messmodelle zusammen führt dies zu Messketten. Eine Messkette ist eine Folge x₁, …, x_n von Messmodellen, so dass der zu bestimmende Teil bt_i des Messmodells x_i in den vorausgesetzten Teil vt_i+1 des „nächsten” Messmodells x_i+1 aus der Messkette eingebettet wird.
Bei einem Messmodell aus einer Messkette wird der zu bestimmende Teil des Messmodells genommen und im darauf folgenden Messmodell der Kette im vorausgesetzten Teil verwen­det.

Fakten und wissenschaftlicher Anspruch

Intendierte Systeme

Von intendierten Anwendungen zu intendierten Systemen

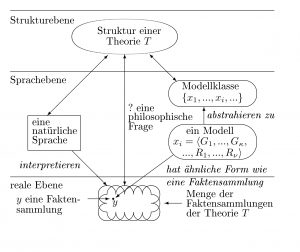
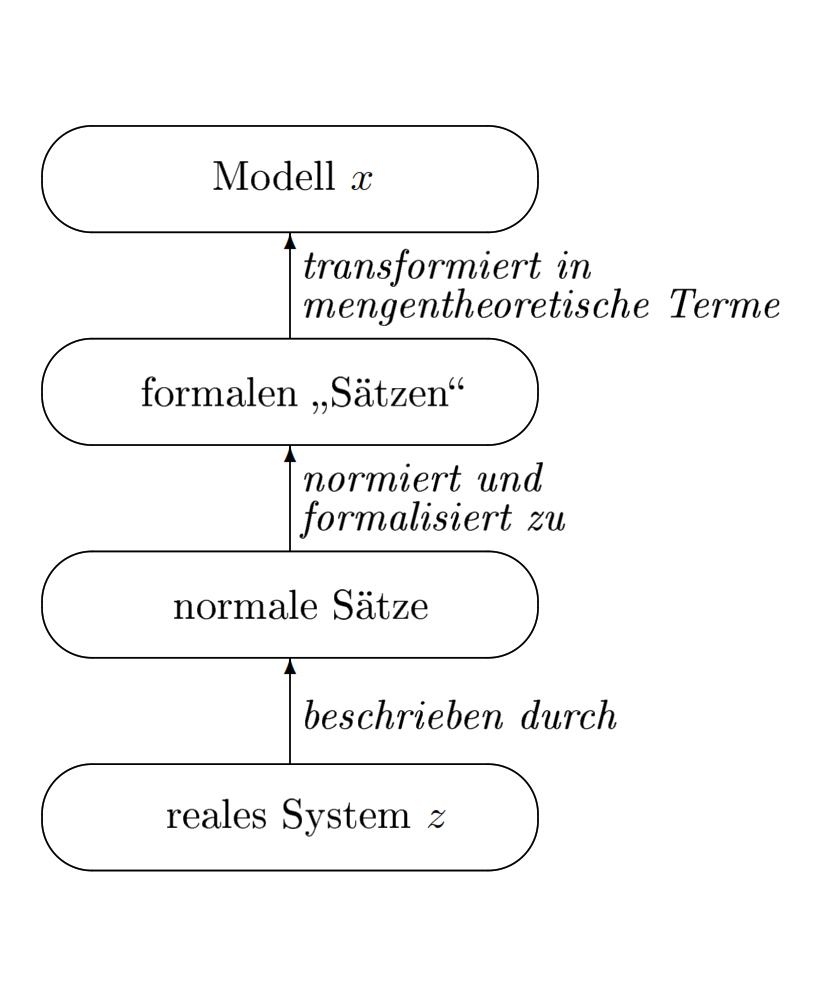
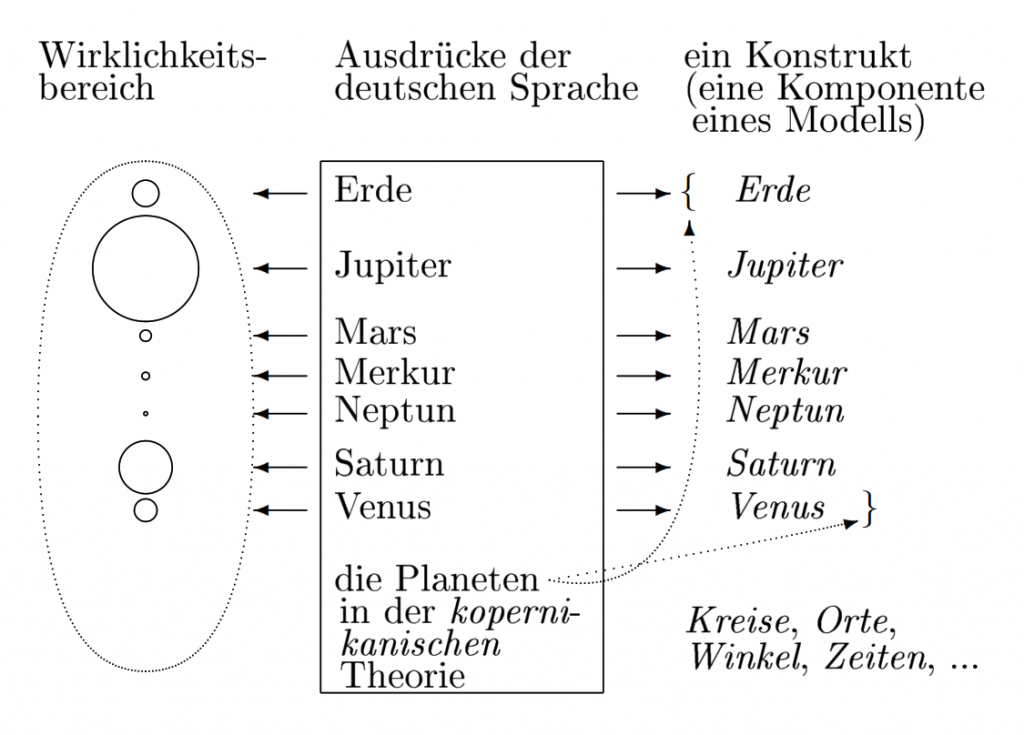
In einer Theorie werden durch Wissenschaftler bestimmte reale Systeme untersucht und mit Modellen beschrieben und erklärt. Im hier verwendeten strukturalistischen Ansatz der Wis­sen­schaftstheorie werden diejenigen Systeme, die Wissenschaftler interessant finden, als in­tended applications (intendierte Anwendungen) bezeichnet. Der Ausdruck «application» be­tont den dynamischen, aktiven Aspekt. Oft wird ein wirkliches System aber nur passiv be­trachtet und untersucht; das System wird nicht angewendet. Zum Beispiel kann in der Gravi­tationstheorie ein schwarzes Loch nicht verändert werden. Wir verwenden daher einen neutra­leren Term und sprechen von intendierten Systemen.
Modelle werden in der Logik dazu verwendet, um Sätze in Modellen zu interpretieren und als gültig zu erweisen. Wenn ein Satz im Modell gültig ist, haben wir ein Indiz, was der Satz be­zogen auf eine bestimmte Situation ausdrücken soll. Wenn dieser Satz in allen Modellen, wel­che die Hypothesen einer Theorie erfüllen, gültig ist, hat sich das was im Satz ausgedrückt wird, weiter verfestigt. Sätze legen auf diese Weise die Modelle der Theorie fest. Allerdings kommen wir damit der Wirklichkeit kaum näher; wir bleiben im Grunde auf der Sprach- und Gedanken­ebene.

Bezug zu wirklichen Systemen

Die Wissenschaftstheorie möchte aber nicht nur über Sprachsysteme und Gedanken sprechen, sondern auch über andere, wirkliche Systeme. Der Bezug zu realen Ereignissen wird in der Wissenschaftstheorie nicht nur den Sprach- und Humanwissenschaften überlassen. In der Wis­senschaftstheorie wird der Bezug zu einem wirklichen System in die jeweilige Theorie verlegt, die es gerade zu untersuchen gilt. Dazu wird neben den Modellen eine weitere Kom­ponente der Theorie verwendet. Diese Komponente verankert die Theorie in wirklichen Ereig­nissen; sie be­steht aus einer Menge von intendierten Systemen und einer dazugehörigen Men­ge von Fakten­sammlungen.
Die Menge I(T) der intendierten Systeme der Theorie T stellt einen direkten Bezug zu wirkli­chen Systemen dar, welche die Forscher aus dem Blickwinkel der Theorie untersucht haben, gerade untersuchen oder in Zukunft untersuchen möchten.

Bestandteile eines intendierten Systems

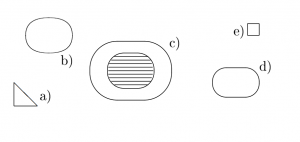
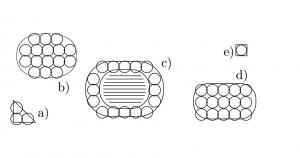
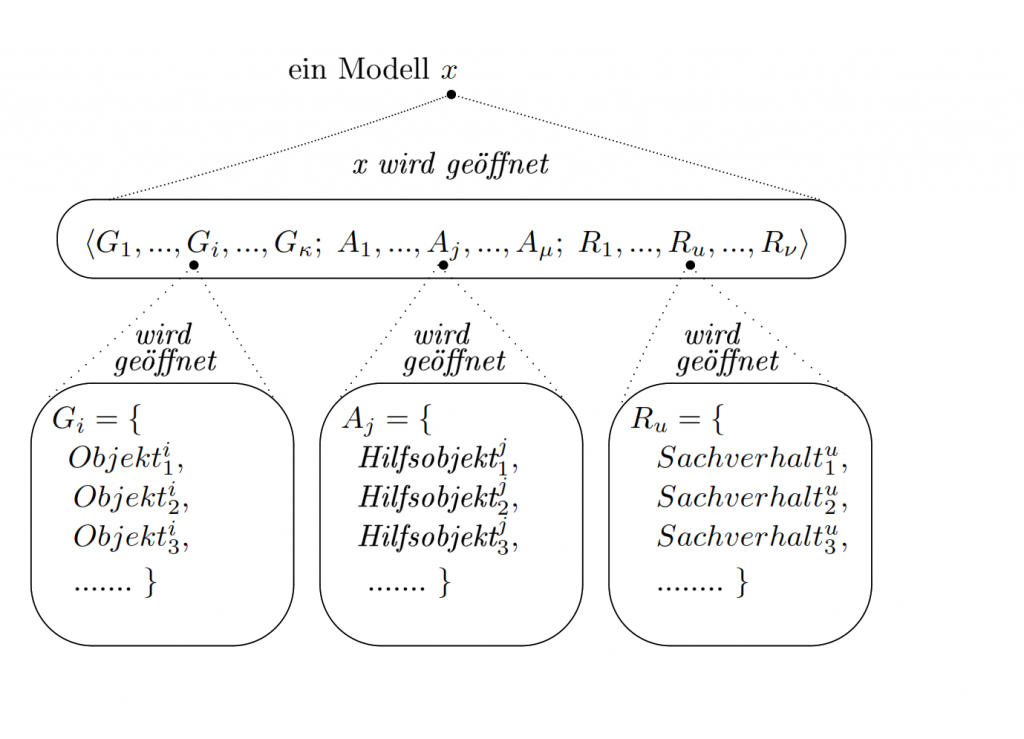
Ein intendiertes System wird durch atomare Terme beschrieben. Dabei bekommt ein inten­dier­tes System immer auch einen Namen oder eine Bezeichnung. Ein intendiertes System kann ähnlich wie ein Modell weiter in elementare Bestandteile zerlegt werden. Bei einer Be­schrei­bung werden auch alle Bestandteile durch atomare Terme repräsentiert. Dabei können die ver­wendeten atomaren Terme in Grundobjekte, Hilfsobjekte und Sachverhalte und die Sachver­halte weiter in verschiedene Relationen eingeteilt werden. Eine Relation wird dabei als eine Menge von Sachverhalten gesehen und ein jeder Sachverhalt liegt genau in einer der Relationen der Theorie.
Oft ist es schwierig zu ent­scheiden, ob ein Ereignis zu einer Grundmenge des intendierten Systems hinzugenommen werden soll oder nicht. Das Problem liegt nicht nur in der approximativen Grenzzie­hung, sondern auch in der zeitlichen Veränderung der Faktenlage. Durch jede Beobachtung, durch jedes Experiment, vergrößert (oder verkleinert) sich das intendierte System. Anders gesagt, ändert sich ein inten­diertes System ständig. Aber es soll gleichzeitig auch «das» reale System darstellen, das bei den Forschern Interesse findet und einen klar bestimmten Namen hat.

Vermeidung von Zweideutigkeit

Der Ausdruck «intendiertes System» wird in zwei Bedeutungen ver­wen­det:

• Einerseits wird ein intendiertes System eindeutig mit einem wirklichen System in Bezie­hung gesetzt, welches sich mit der Zeit im Großen und Ganzen nicht ändert. Es soll eine Form haben, die den Modellen der Theorie ähnelt und die sich aber mit der Zeit nicht ändert.
• Ande­rerseits ändert sich das intendierte System mit der Zeit, wenn durch die laufenden Unter­suchun­gen ständig neue Fakten über das System bekannt werden.

Um diese Zweideutigkeit zu vermei­den, wird jedem intendierten System eine zweite Seite hinzugefügt. Zu jedem inten­dierten System gehört eine Faktensammlung.

Potentielle Modelle

Wiederholung: Was ist ein Modell?

Wissenschaftstheoretisch kann die Menge aller Modelle einer Theorie T kom­pakt und allgemein dargestellt werden.
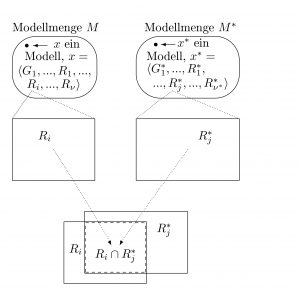
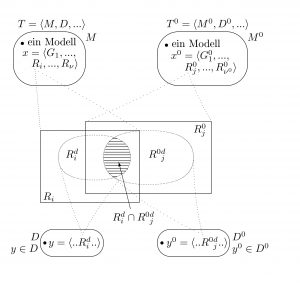
M ist die Menge aller Modelle der Theorie T genau dann wenn für alle x gilt:
x ∈ M genau dann wenn es Mengen G₁, …, G_k, H₁, …, H_m, R₁, …, R_n  gibt, so dass gilt:

• x = 〈 G₁, …, G_κ, H₁, …, H_μ, R₁, …, R_ν 〉 und
• R₁, …, R_ν sind Relationen, die über den Mengen G₁, …, G_κ und H₁, …, H_μ konstruiert sind
• und Hypothese₁ ( G₁, …, R_ν ) und … und Hypothese_n ( G₁, …, R_ν ) gelten.

Genauso kompakt lässt sich ein Modell einer Theorie beschreiben.

• x ist ein Modell der Theorie T genau dann wenn
• x ein Element der Menge aller Modelle der Theorie T ist.

Einführung

Die Modellmenge kann auf verschiedene Weise verallgemeinert werden. Bei einer ersten Verallgemeinerung werden die Definitionen der Modellmenge aller Hypothesen der Theorie weggelassen. Das Resultat wird die Menge der potentiellen Modelle der Theorie T, M_p(T), genannt. Formal ist die Menge M(T) eine Teilmenge von M_p(T):

M(T) ⊆ M_p(T).

Eine Grenzziehung zwischen potentiellen Modellen und Modellen ist damit zwar formal klar, sie wird aber in der Literatur auch auf andere Weise gezogen und bei Rekonstruktionen von Theorien oft nicht genau diskutiert.

Partiell potentielle Modelle und theoretische Terme

Aus einem potentiellen Modell wir ein so genanntes partielles potentielles Modell, wenn einige der Relationen aus dem potentiellen Modell entfernt werden. Dies führt zum Problem der theoretischen Terme. Formal gehen wir von der Liste der Grund­begriffe für die Relationen von T aus und betrachten die Relationen, die an einer be­stimmten Stelle u ( 1 ≤ u ≤ ν ) in den potentiellen Modellen stehen. Die Relation R_u in den po­tentiellen Modellen von T gehört zum entsprechenden Grundbegriff von T. Die Menge all dieser Relati­onen R_u, die bei potentiellen Modellen an der u-ten Stelle stehen, bezeichnen wir durch den Term θ ( R_u ). Dieser Term θ ( R_u ) ist (relativ zu T) T–theoretisch, wenn eine Relation R_u aus θ ( R_u ) nur genauer bestimmt werden kann, indem alle Hypothesen der Theorie T verwendet werden müssen.

Möglichkeitsraum einer Theorie

Einführung

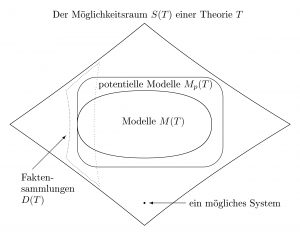
Bei einem potentiellen Modell können einige Komponenten verkleinert, andere vergrößert und wieder andere Komponenten auch völlig entfernt werden. Die Menge aller derartigen Systeme wird als der Möglichkeitsraum der Theorie T, kurz: S(T), benannt. Die Elemente diese Raumes werden Systeme für T genannt.
Eine Theorie T enthält also neben der Menge M(T) der Modelle und der Menge M_p(T) der po­tentiellen Modelle auch den Möglichkeitsraum S(T). Formal gilt, dass die Modellmenge M(T) eine Teilmenge der Menge M_p(T) der potentiellen Modelle ist und M_p(T) eine Teilmenge des Möglichkeitsraums S(T): M(T) ⊂ M_p(T) ⊂ S(T).

Darstellung

Fakten

Erste Facette

Ein Faktum ist in der Beschreibungsebene ein Term.
Ein solcher Term t für ein Faktum kann drei Formen haben:

• t kann ein Name (eine Konstante) sein, die in einer wissenschaftlichen Gruppe homogen verwendet wird. D.h. alle Personen aus einer Gruppe verwenden den Namen für «dieselbe Sache». Der Name bezeichnet ein für die Gruppe klares Ereignis (oder Phänomen, Ding, Tatsache, Sachverhalt). Das Ereignis muss in einem intendierten System der Gruppe wahrgenommen worden sein.
• t kann eine Gleichung sein: ( t₁ = t₂ ), wobei t₁, t₂ induktiv aufgebaute Funktionsterme f ( te₁, …, te_m ) sind, die letzten Endes nur aus Konstanten konstruiert werden.
• t kann die Form eines Sachverhalts p ( t₁, …, t_n ) haben, wobei t₁, …, t_n Funktionsterme sind.

Neben den so konstruktiv bestimmten Fakten gibt es auch theoretische, abgeleitete Fakten. Die nicht abgeleiteten Fakten nennen wir unmittelbare Fakten. t wird aus anderen Fakten und Hypothesen (Sätzen) abgeleitet, wobei t am Ende nur aus unmittelbaren Fakten abgeleitet wird.

Zweite Facette

Ein Faktum «ist» ein reales Ereignis, das von der Gruppe wahrgenommen wird. Das Ereignis muss ein Bestandteil eines intendierten Systems sein.
Ein Faktum wird im allgemeinen auf verschiedene Weise notiert. In Prolog ist es sinnvoll, einen Fakt fakt mit einem Wrapper zu umschließen, z.B. fw(1,typ1,fakt) oder fw(3564756,typ3,faktX).
1 und 3564756 sind «Namen» für Fakten. Diese werden weiter durch Typen wie typ1 und typ3 unterschieden. typ1 kann in einer Anwendung z.B. besagen, dass der fakt eine Person betrifft («ist») und typ3 ein Objekt (keine Person).

Faktensammlungen

Einführung

Eine Faktensammlung besteht lediglich aus Fakten. Ein Faktum kann drei Formen haben. Es kann durch einen atomaren, variablenfreien Satz oder durch eine Liste mit (hybriden) Namen oder durch einen Namen beschrieben werden. Bei allen drei Möglichkeiten soll ein Satz oder ein Name ein wirkliches Ereignis bezeichnen. Meist wird ein Faktum durch ein Prädikat und ein Argument (oder mehrere Argumente) be­schrieben.
An diesem Punkt kommt bei der Beschreibung einer Faktensammlung die Zeit ins Spiel. Ein intendiertes System bleibt zeitlich im Großen und Ganzen gleich. Aber die Menge der Fakten, die aus der Erforschung eines bestimmten intendierten Systems stammt, ändert sich mit der Zeit. Genau die Fakten, die zur Zeit z bekannt und (teilweise) gesichert sind und vom gege­benen System kommen, bilden eine Menge von Fakten. Diese Menge nennen wir die Fakten­sammlung (der Theorie T zum Zeitpunkt z). Eine Faktensammlung bezieht sich immer auf einen gegebenen Zeitpunkt der Theorie T; sie existiert zu einem bestimmten Zeitpunkt.

Aufbau einer  Faktensammlung

Faktensammlungen haben wie Modelle die Form von Listen von Mengen. Eine Faktensamm­lung wird durch eine Liste von Komponenten dargestellt und jede Komponente ist selbst eine Menge von atomaren, variablenfreien Sätzen, Listen oder Namen.
Neben dem Namen verfügt die Faktensammlung über variablenfreie, atomare Ausdrücke, die bestimmte Ereignisse, Objekte, Sachverhalte und andere Aspekte bezeichnen, die innerhalb des Systems bis zu einem bestimmten Zeitpunkt zu finden sind oder dort ablaufen. Alle Be­zeich­nungen für die Entitäten, die bis zum Zeitpunkt z im Inneren des intendierten Systems liegen oder stattfinden und der Name des Systems bilden zusammengenommen die Fakten einer Fak­tensammlung.
Formal können wir eine Faktensammlung zu einem gegebenen Zeitpunkt z so schreiben:

〈 G₁^z, …, G_κ*^z, H₁^z, …, H_μ*^z, R₁^z, …, R_ν*^z 〉.

Faktensammlungen und Modelle

Wissenschaftstheoretisch lassen sich Faktensammlungen und Modelle ziemlich klar trennen. Hypothesen beschreiben Gemeinsamkeiten aller Modelle, während es bei Fakten um einzelne, elementare Bestandteile eines bestimmten Systems geht. Ein Faktum erfasst einen elementa­ren Bestandteil eines intendierten Systems, der direkt wahrgenommen oder in einem konstruktiven Sinn auf wahrnehmbare Ereignisse zurückgeführt werden kann. Eine Hypothese dagegen be­schreibt größere Zusammenhänge vieler Ereignisse. Eine Hypothese enthält meist Ausdrücke wie es gibt oder für alle, welche sich auf variable Weise auf viele verschiedene Dinge und Ereignisse beziehen.
Zum Beispiel ist in der Gravitationstheorie eine Mondfinster­nis zu einem bestimmten Zeitpunkt ein Faktum, dagegen ist eine Gleichung, die alle Zeit­punkte und Orte der Partikel zusammenbringt, eine Hypothese.

Arten von Fakten

Fakten aus einer Theorie T können grob in drei Arten eingeteilt werden:

• Ein Faktum ist für T gesichert, wenn es eine hohe Wahrschein­lichkeit hat, richtig zu sein. Das Ereignis wurde wahrgenommen und gut geprüft.
• Ein teilwei­se gesichertes Faktum wurde zwar wahrgenommen, es wurde aber nicht genau geprüft.
• Bei ver­muteten Fakten müssen andere positive Indizien vorliegen.

Diese Einteilung lässt sich ohne Mühe auch auf Faktensammlungen übertragen. Eine mögliche Faktensammlung oder ein mögliches Faktum wird nur gedanklich bei rein theoretischen Überlegungen über Form und Ähnlichkeit verwendet.

Eingeschränkte Komponenten eines Modells

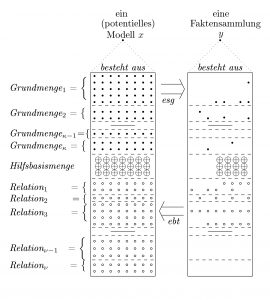
Modelle, Faktensammlungen und Wirklichkeit

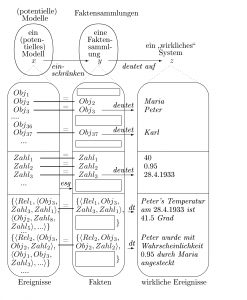
Einbettung und Einschränkung im Möglichkeitsraum

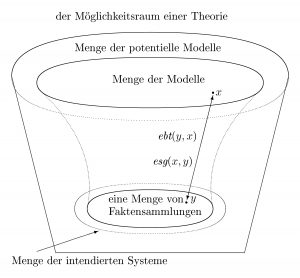
Wissenschaftlicher Anspruch

Einführung

Der Begriff „wissenschaftlicher Anspruch“

In der Wissenschaftstheorie wird üblicherweise der Begriff «empirische Behauptung» (empirical claim) verwendet. Wir verwenden das Wort «Anspruch» und nicht «Behauptung», um die praktische Seite der Wissenschaft zu betonen. Im Weiteren verzichten wir auf das Adjektiv «wissenschaftlich» und sprechen einfach von Ansprüchen.
In der Wissenschaft werden Ansprüche hauptsächlich auf Theorien – Ansichten – bezogen. Eine bestimmte Ansicht erhebt einen Anspruch auf Wahrheit und wenn es eine zweite, ähnliche Ansicht gibt, wird um die Wahrheit gestritten.

Wie kann eine Theorie einen Anspruch erheben?

Im strukturalistischen Ansatz besagt der Anspruch einer Theorie, dass eine Faktensammlung der Theorie zu den Modellen der Theorie passen. Da eine Theorie eine Zeitkomponenten hat, heißt dies:

• Zu jedem Zeitpunkt z, zu dem die Theorie existiert, passt die Menge der Faktensammlungen zu z zur Menge der Modelle der Theorie.

Der Anspruch einer Theorie wird durch Passung formuliert, wobei wir die Hilfsbasismengen in allen Systemen der Theorie implizit lassen. Ein Anspruch lässt sich in mehreren Schritten be­schreiben. Wenn ein Modell x = 〈 G₁, …, G_κ, R₁, …, R_ν 〉 und eine Faktensammlung y = 〈 G₁^z, …, G_κ*^z, R₁^z, …, R_ν*^z 〉 zu einem festen Zeitpunkt z der Theorie gegeben sind, passt y zu x, wenn für alle Grundmengen und Relationen von y folgendes gilt:

• Jede Grundmenge G_i*^z ist eine Teilmenge der «entsprechenden» Grundmenge G_ψ1(i*)
• und jede Relation R_u*^z ist eine Teilmenge der «entsprechenden» Relation R_ψ3(u*).

Eine Faktensammlung passt zu einem Modell

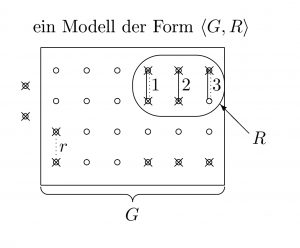
Überprüfung von Hypothesen

Zwei Arten von Hypothesen

Die in der letzten Abbildung allgemein illustrierten Fehler entstehen, wenn Grundelemente und Ereignisse oder Sachverhalte fehlerhaft notiert oder in der Wirklichkeit so nicht anzutreffen sind oder wenn verschiedene Ereignisse durch Hypothesen fehlerhaft miteinander verknüpft sind.
Wir unterscheiden zwei Arten von Hypothesen:

• Eine Hypothese der ersten Art bezieht sich nur auf Ereignisse desselben Typs. Mengentheoretisch gesprochen, sind alle Ereignisse Elemente der­selben Relation.
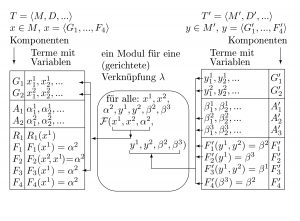
• Bei Hypothesen der zweiten Art werden Ereignisse verschiedener Arten verknüpft. Diese Hypothesen nennen wir Verknüpfungshypothesen (cluster laws). In einer solchen Hypothese werden mindestens zwei Grundrelationen verwendet. Oft gibt es in einer Theorie eine einzige, zentrale Verknüpfungshypothese, in der alle Grundrelationen der Theorie verwendet werden. Das klassische Beispiel ist hier das zweite Newtonsche Axiom, in dem Ort, Zeit, Geschwindig­keit, Beschleu­nigung, Masse und Kraft zu einer unauflösbaren Einheit werden.

Passung einer Faktensammlung zu einem Modell

Wenn die Fakten in einem gegebenen Zeitpunkt vorhanden sind, wird die Passung einer Faktensammlung zu einem gegebenen Modell über die Hypothesen überprüft.
In empirischen Anwendungen wird geprüft, ob eine Hypothese durch die Fakten bestätigt wird. Dieses Bestätigungsverfahren ist immer ein Teil der Passung. Ein solches Verfahren liegt oft weit von einer logischen Ableitung entfernt. Eine Hypothese benötigt oft viele Fakten zur Be­stätigung. Es kann aber sein, dass einige für eine Überprüfung notwendige Fakten in einer Fak­tensammlung einfach nicht vorhanden sind. Oder es kann sein, dass ein atomarer Ausdruck, der ein Faktum beschreibt, den falschen Wahrheitswert hat. Bei Prüfung einer Hy­pothese muss zum Beispiel ein bestimmter Ausdruck falsch sein, um die Hypothese zu bestä­tigen. In an­deren Fällen muss ein Faktum mindestens einmal vorhanden sein, um mit der Prüfung der Hypothese weiter zu kommen.
Eine Faktensammlung passt zu einem Modell, wenn alle Hypothesen und die Fakten zu einem gegebenen Zeitpunkt im Modell gültig sind.

Fehlen von Messmethoden

Besonders heikel wird die Überprüfung einer Hypothese, wenn es zu diesem Zeitpunkt keine Messmethoden für eine bestimmte Relation (für einen bestimmten Begriff) in den Modellen gibt. In diesen Fällen ist ein Grundbegriff der Theorie entweder sehr abstrakt oder der zentrale Grundbegriff der Theorie hat die Funktion, alle Begriffe und Hypothesen zu einem Ganzen werden zu lassen.
Wird ein Begriff in der Theorie nur durch die Hypothesen der Theorie bestimmt, kann dies zum Problem der theoretischen Terme führen.
Zum Beispiel gilt dies für den Begriff der Kraft in der Newtonschen Me­cha­nik oder für den Begriff des Nutzens in der Mikroökonomie. Zumindest in der Anfangs­phase bestimmter, sehr umfassender Theorien, gibt es keine Mess- oder Bestimmungsmetho­den für einen zentralen Begriff. Daher gibt es in diesem Fall nur eine einzige Möglichkeit, bestimmte Werte für diesen Begriff zu erhalten: der Wert muss durch Hypothesen und Fakten abgeleitet werden. Wobei die verwendeten Fakten aber nicht mit dem zentralen Begriff formu­liert werden dürfen.

Passung

Von Hypothesen zu Modellumgebungen

Die verschiedenen Fehlerquellen bei der Überprüfung der Hypothesen führen aber nicht gleich dazu, die gerade verwendeten Hypothesen zu verwerfen. Solche Fehler werden mit Be­dacht zur Kenntnis genommen und dann genauer untersucht. Eine Faktensammlung zur Zeit z passt zwar nicht in Idealform zu einem Modell, sie passt aber oft fast dazu. Oft macht es Sinn, eine Faktensammlung nur approximativ mit einem Modell zur Passung zu bringen.
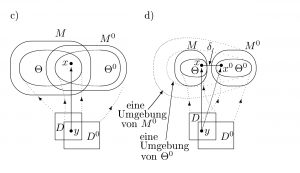
Im Allgemeinen wird Passung so erweitert, dass eine ganze Umgebung des Modells metho­disch verwendet wird. Oft genügt es, ein potentielles Modell zu finden, das nahe am gegebenen Modell liegt. Es wird eine Umgebung des Modells definiert und nach einem potentiellen Mo­dell aus dieser Umgebung gesucht, das zur Faktensammlung passt. Im einfachsten Fall lässt sich eine solche Umgebung durch eine einzige Zahl definieren. Es gibt topologische Metho­den, mit de­nen aus einer Zahl und einem potentiellen Modell eine ganze Umgebung konstru­iert werden kann.

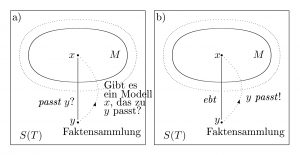
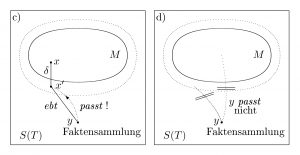
Drei Passungsmöglichkeiten

Von einer zu allen Faktensammlungen

Damit ist die Passung für eine gegebene Theorie aber noch nicht beendet. Nicht eine Faktensammlung zu einem gegebenen Zeitpunkt wird betrachtet, sondern alle Faktensammlungen der Theorie zu diesem Zeitpunkt müssen zu den Modellen passen. Dies eröffnet drei Mög­lichkei­ten:

• Erstens kann es sein, dass jede Faktensammlung zu einem Modell passt: die Theo­rie ist völlig richtig.
• Bei der zweiten Möglichkeit wird jede Faktensammlung mit einem po­tentiellen Modell zur Passung gebracht das nahe bei einem Modell liegt: die Theorie ist mit einer gewis­sen Wahrscheinlichkeit richtig.
• Bei der dritten Möglichkeit gibt es Faktensamm­lungen, die we­der ideal noch approximativ zu Modellen oder potentiellen Modellen passen: die Theorie ist falsch.

Der zweite Fall stellt für anwendungsbezogene Disziplinen den Nor­malfall dar.
Der dritte Fall führt dazu, dass die Theorie verändert wird.

Gehalt einer Theorie

Arten der Einbettung

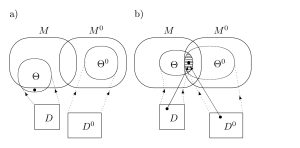
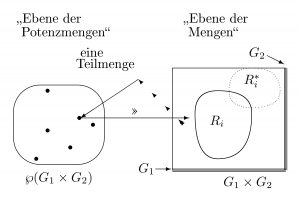
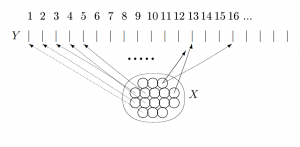
Da die Beziehung der Einbettung ebt einer Faktensammlung in ein Modell im Allgemeinen nicht die Funktionseigenschaften hat, kann es vorkommen, dass verschiedene Faktensysteme in dasselbe Modell eingebettet werden oder dass eine Faktensammlung in verschiedene Mo­delle eingebettet wird. Es kann auch vorkommen, dass es sehr viele Modelle gibt, die zur Pas­sung nicht herangezogen werden. Um diese Punkte zu klären, beginnen wir mit der Menge der Faktensammlungen zu einem gegebenen Zeitpunkt, die in ein Modell eingebettet werden kann. Wir verallgemeinern dann diese Beziehung auf potentielle Modelle und auf mögliche Systeme. Wenn eine Menge X von potentiellen Modellen und eine Menge Y von Systemen gegeben ist, definieren wir, dass die Menge Y von Systemen in die Menge X von potentiellen Modellen eingebettet ist (kurz: Y ebt* X ) genau dann, wenn es für alle Systeme y ∈ Y ein potentielles Modell x gibt, so dass y in x eingebettet ist. Abgekürzt geschrieben:

• ( Y ebt* X ) genau dann wenn es für alle y ∈ Y ein x ∈ X gibt, so dass ( y ebt x) gilt.

Die erste Art der Einbettung (ebt) findet zwischen Systemen statt, die zweite Art (ebt*) zwi­schen Mengen von Systemen.

Definition

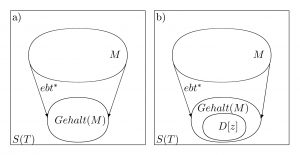
Zu einem gegebenen Zeitpunkt kann nun die Menge von Fakten­sammlungen in die Menge der Modelle der Theorie einbettet werden. In der Mengenschreib­weise lässt sich dies folgendermaßen definieren:

• Der Gehalt(X) von X wird als die Vereinigung aller Y definiert,
  die die Einbettung ( Y ebt* X ) erfüllen:
  Gehalt(X) = ∪ { Y / ( Y ebt* X ) }.

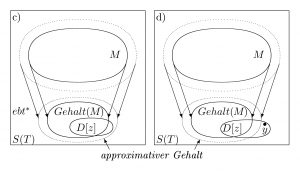
Wenn der Operator Gehalt speziell auf die Menge der Modelle der Theorie angewendet wird, nennt man die Menge Gehalt(M) den Gehalt der Theorie (theory’s content). Der Gehalt der Theorie umfasst alle Systeme, die sich in Modelle einbetten lassen. Den Anspruch der Theorie erhält man, wenn man fragt, ob die Menge der Faktensammlungen, die zu einem Zeitpunkt z gegeben ist, im Gehalt(M) liegt.

Ausgangsposition und 3 mögliche Faktensammlungen

Modellumgebungen

Einführung

Ob die Theorie zu den Faktensammlungen passt, hängt auch vom verwendeten Annäherungsgrad ab, der eine Umgebung für die Modelle festlegt. Wenn ein Umgebungsbegriff verwendet wird, in dem die Umgebung eines Modells durch einen Abstand – oder durch eine einzige, positive Zahl – festgelegt wird, sieht man sofort, dass es wichtig wird, eine ir­gendwie der Realität angemessene Zahl zu verwenden.
Zu einer Theorie gehört normalerweise auch ein Approximationsapparat, mit dem Abstände und/oder Umgebungen bestimmt werden können. Die Bestimmung und Untersuchung von Abständen und Umgebungen wird in jeder wissenschaftlichen Disziplin anders gehandhabt.
In der Wissenschaftstheorie müssen Abstände und Umgebungen auch wissen­schaftsübergreifend untersucht werden müssen. Es reicht nicht aus, den Approximationsappa­rat einer bestimmten Theorie zu kennen und anwenden zu können. Beim Ver­gleich zweier Theorien müssen auch die eventuell verschiedenen statistischen Begriffe und Methoden beach­ten. Daher sind die Begriffe des Abstands und der Umgebung so zu beschreiben, dass sie für alle Theorien verwendet werden können. Die speziellen Abstands- und Umgebungsme­thoden einer bestimmten Theorie lassen sich dann unter die in der Wissenschaftstheorie all­gemein be­handelten Begriffe subsumieren.

Definition einer Umgebung ohne Abstandsbegriff

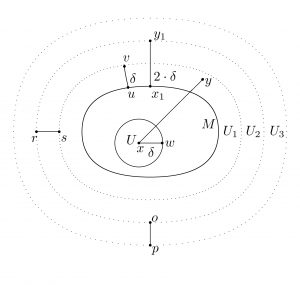
Im Folgenden wird das einfachste Umgebungssystem für einen Punkt x0 dargestellt, bei dem weder Ab­stände noch Uniformitäten verwendet werden. Dieses System besteht aus drei Komponenten, aus einer Menge P von Punkten, aus einem ausgezeichneten «Ursprungspunkt» x₀ und aus einer Menge U von Umgebungen von x₀: UR = 〈 P, x₀, U 〉. Eine Umgebung u aus U besteht aus einer Menge von Punkten, die alle in einer Umgebung des Ursprungspunkts x₀ liegen. Ob eine Menge von Punkten u eine Umgebung von x₀ ist, hängt entscheidend davon ab, ob u zur Menge U aller Umgebun­gen von x₀ gehört oder nicht. Das heißt, ein Umgebungssystem enthält nur eine bestimmte Auswahl von Umgebungen, die durch folgende Hypothesen sehr allgemein charakterisiert wird:

• Jede Obermenge einer Umgebung von x₀ ist Umgebung von x₀.
• Der Durchschnitt endlich vieler Umgebungen von x₀ ist eine Umgebung von x₀, und P ist eine Umgebung von x.
• Jede Umgebung von x₀ enthält x₀.
• Ist u Umgebung von x₀, so gibt es eine Umgebung v von x₀ derart, dass u Umge­bung jedes Punktes von v ist.

Definition einer Umgebung mit Abstandsbegriff

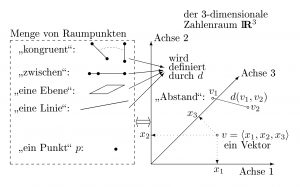
Der Umgebungsbegriff kann auch durch eine Abstandsfunktion d definiert werden. Durch diese Funktion bekommen je zwei Punkte a und b aus P eine nicht negative, reelle Zahl α zugeordnet: d ( a, b ) = α. Die Menge ℜ⁺₀ dieser nicht negativen, reellen Zahlen wird dabei als bekannt vorausgesetzt. Das bedeutet, dass die verschiedenen Hypothesen, welche die Menge der reellen Zahlen charakterisieren, nicht explizit angegeben werden. Für die Abstandsfunk­tion d werden folgende Hypothesen verwendet:

• Es ist stets d ( a, a ) = 0, und aus d ( a, b ) = 0 folgt a = b.
• Für je zwei Punkte a, b gilt d ( a, b ) = d ( b, a ).
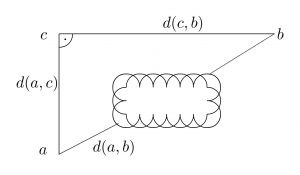
• Für je drei Punkte a, b, c gilt: d ( a, c ) ≤ d ( a, b ) + d ( b, c ).

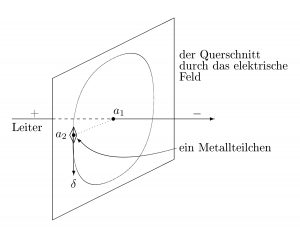
Ausgehend von einem Punkt a₀ und einer nicht negativen, reellen Zahl α wird mit Hilfe der Abstandsfunktion d eine Umgebung u wie folgt definiert:
  u =  { b / b ∈ P und d ( a₀, b ) ≤ α }.

Verschiedene Modellumgebungen

Modelle

Einführung und Definition

Von einem realen System zu einem Modell

Bestandteile eines Modells

Ein Modell wird in zwei Schritten genauer beschrieben:

• Im ersten Schritt werden die Bestand­teile des Modells in ihre elementaren Teile zerlegt.
• In einem zweiten Schritt lassen sich aus den elementaren Bestandteilen einfache und komplexe Teile des Modells zusammensetzen.

Einfa­che Bestandteile eines Modells werden Fakten und komplexe Teile Hypothesen genannt. Diese Unterscheidung wird auch auf der Beschreibungsebene getroffen.
Alle Bestandteile eines Mo­dells werden durch Terme beschrieben: Fakten durch einfache Terme und Hypothe­sen durch komplexe Terme. Fakten bilden in der Wirklichkeit vorhandene Ereignisse ab, die in der gerade untersuchten Situation Grundbestandteile des Modells sind und die nicht weiter analysiert wer­den. Hypothesen repräsentieren Gesamtheiten von Ereignissen, die in einem Modell eine Ein­heit bilden.

Definition eines Modells

Ein Modell ist eine Liste von Mengen. Eine solche Menge nennen wir auch eine Komponente (des Modells, der Liste). Es werden drei Arten von Mengen in einem Modell unterschieden: Basismengen, Hilfsbasismengen und Relationen:
Eine Basismenge enthält Objekte oder Dinge oder auch elementare Ereignisse. Ereignisse nennen wir elementar, wenn sie für die Theorie nicht weiter in kleinere Einzelteile zerlegt werden.
Eine Hilfsbasismenge besteht aus mathematischen Objekten (Zahlen oder abstrakteren Dingen).
Eine Relation R ist eine Menge von Listen, die durch eine „Bezeichnung“ (z.B. durch ein Prädikatsymbol) der Relation zusammengehalten wird. Ein Element einer Relation besteht aus einer Liste von Variablen, die verschiedene Typen haben können. Eine solche Variable läuft über einen Bereich. Der Bereich enthält Fakten und auch „mögliche Fakten“.
Z.B. ist p die Bezeichnung (das Prädikatssymbol) und fakt₁, …, fakt_n sind mögliche Fakten.
<p, fakt₁, …, fakt_n> ist eine Liste und ein Element der Relation R mit
R = { x | es gibt fakt₁, …, fakt_n so dass x = <p, fakt₁, …, fakt_n> }
Woher kommen diese Entitäten?
p kann z.B. das Verb mag sein. Wenn die „variablen Fakten“ fakt₁, …, fakt_n durch Namen wie „Peter“, „Susi“, „Monika“, „Hans“ und n durch 4 ersetzt werden, erhalten wir einen Satz. Inhaltlich gesprochen läuft eine Variable über Namen, oder anders gesagt über eine offene Menge von Personen. Wir haben eine Vorstellung, wie diese erörterte Personenmenge begrenzt ist.

Ein Modell x hat also die Form x = <G₁, …, G_k, A₁, …, A_m, R₁, …, R_n>

wobei G₁, …, G_k Mengen von Basismengen,
A₁, …, A_m Mengen von Hilfsbasismengen
und R₁, …, R_n Relationen sind.

Der Begriff des Modells wird in der Logik genauer definiert. Wir beschränken uns hier darauf, den Modellbegriff durch Beispiele zu erläutern.

Ein Modell besteht aus Mengen und Elementen

Die Balancetheorie von Heider

• Kurze Beschreibung in Wikipedia.
• YouTube-Video.
• Detaillierte Beschreibung mit strukturalistischer Rekonstruktion und Modellierung in Prolog als PDF-Datei (© Dr. Klaus Manhart).

Abbildung von Modellen in Prolog – Erste Schritte

mag(peter, susi).                       /* Peter mag Susi */
mag(X, susi).                           /* Jeder mag Susi */
mag(peter, Y).                          /* Peter mag jeden */
mag(peter, Y), mag(Y, peter).           /* Peter mag jeden und jeder mag Peter */
mag(peter, susi); mag(peter, monika).   /* Peter mag Susi oder Peter mag Monika */
not(mag(peter, pizza)).                 /* Peter mag keine Pizza */
mag(peter, susi) :- mag(peter, monika). /* Peter mag Susi wenn Peter Monika mag */

/* X und Y sind Freunde wenn sie sich gegenseitig mögen */
freunde(X, Y) :- mag(X, Y), mag(Y, X).

/* X hasst Y wenn X Y nicht mag*/
hasst(X, Y) :- not(mag(X, Y)), !.

/* X und Y sind Feinde wenn sie sich gegenseitig nicht mögen */
feinde(X, Y) :- not(mag(X, Y)), not(mag(Y, X)), !.

Verwendete Konstrukte und Prädikate

• und: :Goal1, :Goal2 (,/2)
• oder: :Goal1; :Goal2 (;/2)
• nicht: not(:Goal) (not/1)
• cut: ! (!/0)
• asserta: asserta(+Term) (asserta/1)

Sprachen und Ausdrücke

Wissenschaft und Wissenschaftstheorie werden durch Sprachen mitgeteilt und beschrieben.  Ohne Sprache gibt es keine Wissenschaftstheorie. Aber sind Sprachen auch zentrale Bestand­teile der Wissenschaftstheorie?

Es gibt drei Arten von Sprachen: natürliche, universale und formale Sprachen. In einer Spra­che werden viele verschiedene Arten von Ausdrücken benutzt, die je nach Situation bestimm­ten Bereichen zugeordnet werden.

Die natürlichen Sprachen sind für die Wissenschaftstheorie durchaus relevant. Es ist aber auch klar, dass eine natürliche Sprache kein zentraler Bestandteil der Wissenschaftstheorie sein kann. Das schlagende Argument hierfür lautet: die meisten Wissenschaftler können die anderen Spra­chen, in denen viele der Menschen über Wissenschaft sprechen, nicht verstehen.

Für die Wissenschaftstheorie ist es sinnvoll, zwei sprachliche Ebenen zu unterscheiden. In der universellen Ebene wird ein Sprachfragment nur für abstrakte Formen benutzt. Erst in der Ebene der vielen verschiedenen Wissenschaften und Theorien wird jeweils eine spezielle for­male Sprache verwendet – je nach Anwendungsfall einer Theorie.

Für diese Vorgehensweise sind die mengentheoretischen Sprachen besonders gut geeignet. Der men­gentheoretische Rahmen lässt einerseits Platz für alle wissenschaftlichen Inhalte. Dieser Rah­men kann für die Mathematik ebenso gut verwendet werden, wie für Politologie oder Herme­neutik. Auf der anderen Seite kann bei der Beschreibung eines bestimmten intendierten Systems mengentheoretisch immer weiter sowohl in abstraktere als auch in konkretere Ebe­nen vorge­stoßen werden.

Mengentheoretische Terme sind inzwischen auch oft in der Wissenschaftstheorie anzutref­fen. Terme für Entitäten wie: Modelle, intendierte Systeme, Fakten, Theorienentwicklungen, reelle Zahlen und vieles mehr – werden immer durch atomare Bestandteile konstruiert. Einige dieser atomaren Ausdrucksformen sind in der folgenden Tabelle zusammengestellt:

Ein Ereignis lässt sich auf viele verschie­dene Weisen und in verschiedenen Sprachen ausdrücken. In der nächsten Abbildung sind Ausdrücke aus zwei natürlichen Sprachen S₁, S₂ zu sehen. Einige hervorgehobene Ausdrü­cke, die aus verschiedenen Beschreibungsebenen stammen, bezeichnen alle dasselbe reale Er­eignis e. Zwei Rechtecke stellen zwei Sprachen dar, die in drei Beschreibungsebenen unterteilt sind. Die Punkte in den Rechtecken stellen Ausdrücke dar. Punkte im Oval der Abbildung sind graphisch dargestellte, reale Ereignisse. Diese Ereignisse werden normaler­weise nicht wahrgenommen. Ein bestimmtes Ereignis e ist durch einen schwarzen Punkt her­vorgehoben. In den Rechtecken sind einige Ausdrücke ebenfalls durch schwarze Punkte dar­gestellt und mit Symbolen aⁱ_j(e) bezeichnet. Der untere Index j läuft über die beiden Spra­chen, der obere Index i über Ausdrucksebenen. Der rechts eingezeichnete, dick gepunktete Pfeil deutet an, dass wei­tere Sprachen hinzugefügt werden können. Auf ähnliche Weise be­sagt der dick gepunktete Pfeil oben links, dass weitere Ausdrucksebenen vorhanden sein könnten. Die dünn gepunkteten Pfeile bedeuten, dass ein Ausdruck aⁱ_j(e) ein bestimmtes Er­eignis e be­zeichnet. Im Beispiel deuten alle schwarz hervorgehobenen Ausdrücke aⁱ_j(e) auf dasselbe rea­le Ereignis e. Das Er­eignis e, welches durch die drei symbolischen Ausdrücke a¹₁(e), a²₁(e), a³₁(e) bezeichnet wird, lässt sich in der deutschen Sprache auf verschiedene Weise ausdrü­cken. Auf einer ersten, tech­nischen Ebene könnte zum Beispiel der Ausdruck Umwandlung von Kohle in Energie benutzt werden. Auf einer ökonomischen Ebene wäre der Ausdruck Produktion von Strom durch das Unternehmen RWE treffend und auf ökologischer Ebene könnte der Ausdruck Einbringen von Schadstoffen in die Atmosphäre verwendet wer­den. Auf ähnliche Weise lassen sich die Aus­drücke a¹₂(e), a²₂(e), a³₂(e) in der englischen Sprache for­mulieren. Ein Beispiel für einen über­lappenden Ausdruck a¹₂(e) wäre zum Bei­spiel googeln.

Diese linguistische Situation wird durch eine wissenschaftliche Anwendung genauer erläutert. In der folgenden Abbildung ist im unteren Bereich ein reales System aufgeführt – ein mechanischer Stoß – wie er in der klassischen Mechanik untersucht wird. Man sollte sich hierbei den gezeich­neten Stoß als tatsächlich stattfindend vorstellen und ihn direkt wahrnehmen. Ein schwarz dar­gestelltes, „schweres” Partikel stößt mit einem weißen, „leichten” Partikel auf einer gera­den Linie zusammen. Diese experimentelle Anordnung ist in der Literatur oder im Internet oft zu finden. Um die räumlichen Abstände zu messen, steht ein Stab, ein Metermaß, parallel zur Stoßebene und eine per Hand startbare Uhr bereit. Diese Uhr ist durch eine t-Achse repräsen­tiert.

Links oben sind die wichtigsten Ausdrücke, mit denen dieses Ereignis physikalisch beschrie­ben werden kann, in deutscher Sprache notiert. Rechts oben ist eine ähnliche Liste mit Aus­drücken in englischer Sprache zu sehen. Von einigen Ausdrücken führen gepunktete Pfeile zu den ent­sprechenden Teilen oder Teilprozessen, die im ablaufenden Stoß vorhanden sind. So deutet beispielsweise der Ausdruck schwarze Kugel auf die im Stoß zu sehende schwarze Ku­gel hin: der Ausdruck bezeichnet einen materielle Gegenstand. Der Ausdruck Stoß deutet auf ein Er­eignis. Der Ausdruck Dimension kann nicht direkt auf etwas Konkretes hindeuten. Ein Aus­druck dieser Art wird sprachlich normalerweise auf andere Ausdrücke zurückgeführt. Der in der Abbildung eingezeichnete Pfeil unten links besagt, dass die Ausdrücke im realen Sys­tem eine bestimmte Bedeutung haben.

Begriffe

Begriff: Einführung

Was ist ein Begriff?

Begriff – etymologisch vom Stammwort greifen abgeleitet – bedeutet:

• In erster Näherung eine Vorstellung einer Sache, die zum Greifen nahe ist und die durch Sprache ausgedrückt werden kann.
• In zweiter Näherung, bevor die Mengenlehre auf den Plan trat, wurde der Begriff in Um­fang und Inhalt unterteilt.
• In dritter Näherung wurden schließlich auch Mengen be­nutzt. Der Umfang eines Begriffs wird als eine Menge vorgestellt; die Elemente dieser Menge fallen unter diesen Begriff.

Auch beim Inhalt eines Begriffs werden weitere Bestandteile, wie syntaktische, paradigmatische und semantische Elemente unterschieden. Hauptsächlich durch psychologische Untersuchungen wurde klar, dass dem Begriff ein be­grifflicher Raum (conceptual space) zugeordnet werden muss, der auch mehrere Dimensio­nen haben kann. Zum Beispiel werden beim Begriff des Raumes norma­lerweise drei räumliche Dimensionen unterschieden. Bei einem anderen Ansatz, wird der Inhalt eines Begriffs durch sprachliche Ausdrücke und Konstrukte dargestellt.

Der “Tripelansatz” von Kuznetsov

Definition

Im „Tripelansatz” von Kuznetsov besteht ein Begriff B aus drei Komponenten, nämlich aus dem Wirklichkeitsbereich W des Begriffs, aus einer Gesamtheit K von Konstrukten des Be­griffs und aus einer Menge E von sprachlichen Ausdrücken (englisch: expression) für den Begriff:

B = 〈 W, K, E 〉

Diese drei Komponenten liegen in verschiedenen Dimensionen: die Ausdrücke in der Sprach­dimension, die wirklichen Ereignisse in der Wirklichkeitsdimension und ein Konstrukt in der Dimension der Mengen.

Eine Menge ist philosophisch gesehen eine Art Zwitter. Sie enthält einen Sprachanteil und ei­nen „natürlichen” Anteil, der unabhängig von menschlicher Wahrnehmung existiert. Die Menge der Planeten zum Beispiel wird einerseits von einer Person mental erfasst und durch Worte ausgedrückt. Andererseits sind die meisten Menschen der Meinung, dass es viele ver­schiedene Planeten, wie zum Beispiel unsere Erde und die Venus – also eine Art von Gesamt­heit – auch geben würde, wenn die Menschheit nicht existieren würde.

Der Wirklichkeitsbereich W des Begriffs besteht aus einer sehr großen Menge von Ereignis­sen („Phänomenen”), über die ohne Sprache nichts ausgesagt werden kann. Ein solches Er­eignis ist etwas, das letztlich nur durch eine Person wahrgenommen wird oder zu einem frühe­ren Zeit­punkt wahrgenommen wurde. Weitere abstrakte, konstruierte oder rein gedachte Phä­nomene lassen sich immer von den direkt wahrgenommenen Ereignissen ableiten. Zum Bei­spiel nimmt eine Person zu einem Zeitpunkt und an einem bestimmten Ort ein Ereignis wahr, welches sie durch den Ausdruck die Venus geht gerade auf äußert.

Ein Konstrukt aus K ist eine Komponente eines Modells einer Theorie T, wobei das Konstrukt zu einem bestimmten Begriff der Theorie T gehört. Ein Modell hat die Form

〈 G₁, …, G_k, A₁, …, A_m, R₁, …, R_n 〉

wobei G₁, …, G_k die Grundmengen, A₁, …, A_m  die Hilfsbasismengen und R₁, …, R_n die Relationen des Modells sind. Ein Konstrukt kann die Form einer Grundmenge oder einer Relation des Modells haben, es kann aber auch durch die Grundmengen und Relationen defi­niert sein – in einfacher oder komplexer Weise.

Die dritte Komponente E eines Begriffs enthält einerseits Ausdrücke, die auf Ereignisse deu­ten, welche unter den Begriff fallen. Ein solcher Ausdruck kann ein Name oder eine ausführ­lichere Beschreibung eines Objekts oder eines Phänomens sein. Andererseits enthält E Aus­drücke, die den Begriff „als Ganzes” bezeichnen. Die Ausdrücke der letztgenannten Art be­zeichnen abs­trakte, allgemeine Sachverhalte. Ein solcher Ausdruck enthält zwingend auch mindestens eine Variable, nämlich für die Ereignisse, die unter diesen Begriff fallen. Unter den Ausdrücken finden wir normalsprachliche Terme, Sätze und Phrasen, wie Hartz IV; Die Erde kreist um die Sonne; oder der helle Abendstern. In wissenschaftlichen Beschreibungen spielen zusätzlich Va­riablen eine wichtige Rolle, mit denen verschiedene mögliche, in Wirk­lichkeit aber nicht statt­findende Ereignisse erörtert und beschrieben werden. Bei einem Term, einem Satz und einem Ausdruck kann man ein Substantiv eventuell an mehreren Stellen durch eine Variable ersetzt. Aus einem Satz entsteht auf diese Weise eine sogenannte Formel. Eingeschränkt auf eine bestimmte Theorie und einen bestimmten Begriff, der zu dieser Theo­rie gehört, lässt sich ein Ausdruck angeben, welcher die Menge aller Konstrukte des Begriffs be­inhaltet. Die einzelnen Konstrukte des Begriffs sind Teile von Modellen dieser Theorie. Der so abstrakt umschriebene Bereich charakterisiert somit den Inhalt des Begriffs durch ein mengen­theoretisches Prädikat.

Beziehung zwischen den drei Komponenten

Die drei Komponenten eines Begriffs werden durch drei Beziehungen zusammengehalten:

• Bei der ersten Beziehung deutet ein Ausdruck auf ein wirkliches Ereignis.
• Bei der zweiten Bezie­hung bezeichnet ein Ausdruck – situationsabhängig – ein Konstrukt.
• Bei der dritten Beziehung passt ein Konstrukt zu dem Wirklichkeitsbereich.

Alle drei Beziehungen werden in vielen Dis­ziplinen, wie zum Beispiel Philosophie, Psychologie, Kognitionswissenschaft, Linguistik und Informatik genauer untersucht.

Ein Begriff B und seine drei Komponenten W, K und E.

Strukturelle Ähnlichkeit von Theorien und Begriffen

Es ist deutlich zu erkennen, dass Theorien und Begriffe strukturell ähnlich sind:

• Die Menge der Faktensammlungen einer Theorie entspricht dem Wirklichkeitsbereich eines Begriffs.
• Die Modelle entsprechen den Konstrukten.

Ein Unterschied zwischen Begriffen und Theorien besteht darin, dass bei den Begriffen die normalen Sprachen eine größere Rolle spielen als bei den Theorien.

Begriff: Beispiele

Der Begriff die Planeten in der kopernikanischen Theorie

Der Begriff des Nutzens

Dieser Begriff liegt in der Wissenschaft weit weg von der Beobachtungsebene. Einen Nutzen können wir nicht direkt wahrnehmen. Trotz­dem spielt er in der heutigen Weltsicht eine zentrale Rolle; alle Handlungen der Menschen werden so gedeutet, dass sie einen möglichst großen Nutzen haben sollen. Der Begriff des Nut­zens ist von einem anderen Typ als zum Beispiel der der Sonne. Nutzen ist in der Grund­bedeu­tung eine relationale Beziehung zwischen einer Person und den Gegenständen, die sie besitzt oder besitzen möchte. Je mehr Dinge eine Person besitzt, desto mehr Nutzen kann die Person (normalerweise) aus diesen ziehen – desto mehr Nutzen hat sie. Dieser Begriff wird heute in vielen verschiedenen Bedeutungsvarianten verwendet. Sowohl der Wirklichkeitsbe­reich als auch das Konstrukt ist nicht einfach zu beschreiben.

In der deutschen Sprache werden Ausdrücke verwendet wie: Nutzen, Nutzenfunktion, Nutzen­funktion einer Person in einer Situation, und viele weitere. Das Substantiv Nutzen bezeichnet ein schwer verständliches, wirkliches Objekt. Über den Wirklichkeitsbereich des Begriffs lässt sich ohne Worte wenig sagen. Der Begriff bekommt mehr Inhalt, wenn wir durch die Sprache mehr über die Wirklichkeit und über ökonomische Modelle erfahren.

Wissenschaftstheorie

Neues Buch als Grundlage

Was ist anders im neuen Buch?

• Einfacher, normalsprachlicher Einstieg.
• Thema «Struktur» erscheint erst in späteren Kapiteln.
• «Ereignis» als zentrale Komponente von Theorien.
• Aufnahme des Themas «Wahrscheinlichkeit».
• Ca. 80 anschauliche Abbildungen.
  
• Das Buch begleitende Website
  • theory-of-science.com
  • mit über 120 Übungen
  • und zusätzlichen Informationen.

Inhaltsverzeichnis

Übungen

• Beispiel 1
• Beispiel 2

Was ist Wissenschaftstheorie?

Wir verstehen Wissenschaftstheorie auf die folgende Weise:
Sie untersucht sowohl statisch als auch dynamisch Theorien, Theoriennetze, Strukturen, Modelle für Wirklichkeitsbereiche, die dazugehörigen Bestimmungs- und Messmethoden und allgemeinere Methoden und Prozesse, die in den Theorien verwendet werden. Solche Untersuchungen gehen von wissenschaftlichen Theorien und Netzen als intendierte Systeme für die Wissenschaftstheorie aus.

Wissenschaftliche Disziplinen

Die Wissenschaft ist in viele verschiedene Disziplinen aufgeteilt. In jeder Disziplin gibt es verschiedene Wissensbereiche.

Ein Wissensbereich wird zusammengehalten

• erstens durch eine Theorie (oder ein Theoriennetz) und
• zweitens durch eine Gruppe von Wissenschaftlern, welche bestimmte Systeme erforschen, die sie interessant finden. Wir reden im Folgenden von der Gruppe, d.h. einer Menge von Personen, die eine bestimmte Theorie untersucht oder untersuchen möchte.

Komponenten einer Theorie

Eine Theorie enthält verschiedene Komponenten. Die beiden wichtigsten sind die sog. intendierten Systeme (oder intendierten Anwendungen) und die theoretischen Modelle, die in dieser Theorie entwickelt wurden. Die Modelle werden durch Sätze (Terme) bezeichnet oder charakterisiert. Jede Theorie hat eine abgegrenzte Menge von Termen. Wir nennen diese Terme die Terme der gegebenen Theorie.

In der Mathematik ist ein Term ein sinnvoller Ausdruck, der Zahlen, Variable, Symbole für mathematische Verknüpfungen und Klammern enthalten kann. Terme sind die syntaktisch korrekt gebildeten Wörter oder Wortgruppen in der formalen Sprache der Mathematik.

Die wichtigsten Ebenen einer Theorie

• Theorienentwicklungen
• Theoriennetze
• Theorien
• Sprachen
• Modelle
• intendierte Systeme
• Fakten
• Ereignisse

SWI-Prolog

Entweder lokal installieren (siehe z.B. die folgende Installationsanleitung)
– oder –
online nutzen (siehe: SWISH).

Entwicklungsumgebungen für SWI-Prolog

In SWI-Prolog vorhandene Entwicklungswerkzeuge

• Program Development Tools

IDE-Plugins für SWI-Prolog

• PDT für Eclipse.
• VSC-Prolog für Visual Studio Code.

Abbildungen von Theorien in Prolog – Erste Schritte

theorienliste([theoriename1,theoriename2,theoriename3,theoriename5]).
theorie(theoriename1,[modell1,intsystem1]).
theorie(theoriename1,[modell1,intsystem2]).
theorie(theoriename2,[modell2,intsystem3]).
theorie(theoriename2,[modell2,intsystem4]).
theorie(theoriename2,[modell2,intsystem5]).
theorie(theoriename5,[modell5,intsystem6]).
theorie(theoriename5,[modell5,intsystem3]).

theorie(N,M,I) :-
	theorienliste(U),
	member(N,U),
	theorie(N,X),
	X = [M,I].

Beispielabfragen

?- theorie(Name,Modell,IntSystem).

Name = theoriename1,
Modell = modell1,
IntSystem = intsystem1 ;
Name = theoriename1,
Modell = modell1,
IntSystem = intsystem2 ;
Name = theoriename2,
Modell = modell2,
IntSystem = intsystem3 ;
Name = theoriename2,
Modell = modell2,
IntSystem = intsystem4 ;
Name = theoriename2,
Modell = modell2,
IntSystem = intsystem5 ;
Name = theoriename5,
Modell = modell5,
IntSystem = intsystem6 ;
Name = theoriename5,
Modell = modell5,
IntSystem = intsystem3.

?- findall(W,theorie(theoriename2,W),Liste).

Liste = [[modell2, intsystem3], [modell2, intsystem4], [modell2, intsystem5]].

Verwendete Konstrukte und Prädikate

• Liste: []
• Element einer Liste: member/2
• Gleichheit: =/2
• Sammle alle Lösungsinstanzen in einer Liste: findall/3

Seminareinführung

Grundbestandteile der Wissenschaft

• Ereignisse
  • konkret und abstrakt
  • können zu Ereignisarten zusammengefasst werden
  • können aus Komponenten (oder Dimensionen) bestehen
• Elemente
  • als Teile einer Gesamtheit
• Beziehungen
  • konret und abstrakt
  • können zu Beziehungstypen zusammengefasst werden

Artikel zu «Wissenschaftstheorie» im Internet

• Wissenschaftstheorie
• Strukturalistisches Theorienkonzept

NetLogo

• Homepage

Zur Einführung in Prolog

• Eine kurze Einführung in Prolog
• Learn Prolog Now!
• Learn Prolog Now! (für SWI-Prolog)

Informationen zu SWI-Prolog

• Homepage
• Entwicklungswerkzeuge
• Portable App (nur für Micosoft Windows)
• Webbasierte Version (mit eingeschränktem Funktionsumfang)
• Einführung in die Logische Programmierung und SWI-Prolog

Forschungsgruppe

• The Munich Simulation Group

Literatur

Wissenschaftstheorie

Bücher

• Balzer, W., Moulines, C. U., Sneed, J. D. (1987) An Architectonic for Science
• Balzer, W., Sneed, J. D., Moulines, C. U. (2000) Structuralist Knowledge Representation: Paradigmatic Examples
• Balzer, W. (2009) Die Wissenschaft und ihre Methoden
• Balzer, W., Brendel, K. R. (2019) Theorie der Wissenschaften

Zeitschriften

• Erkenntnis
• Journal for General Philosophy of Science
• Synthese

Simulation

• Balzer, W., Kurzawe, D., Manhart, K. (2014) Künstliche Gesellschaften – mit PROLOG (Website)
• Wilensky, U., Rand, W. (2015) An Introduction to Agent-Based Modeling

Prolog

• Clocksin, W. F., Mellish, C. S. (2003) Programming in Prolog: Using the ISO Standard
• Blackburn, P., Bos, J., Striegnitz, K. (2006) Learn Prolog Now!

Open Access

• JASSS – The Journal of Artificial Societies and Social Simulation
• SSOAR – Social Science Open Access Repository

Geplanter Seminarablauf

Themen

• Grundbestandteile der Wissenschaft
• Wissenschaftstheorie
• Sprachen und Begriffe
• Modelle
• Fakten und wissenschaftlicher Anspruch
• Messung – fundamental und modellgeleitet
• Wissenschaftstheorie und Wahrscheinlichkeit
• Struktur und Invarianz
• Entstehung und Änderung von Theorien
• Theorienvergleich
• Theoriennetze
• Eine Theorie der Wissenschaften

Aufgaben

Literatur

1) Balzer, W., Kurzawe, D., Manhart, K. (2014) Künstliche Gesellschaften – mit PROLOG.

2) die Website für NetLogo, und das dazugehörige Benutzerhandbuch.

3) Balzer, W., Brendel, K. R. (2019) Theorie der Wissenschaften.

4) Balzer, W. (2009) Die Wissenschaft und ihre Methoden.

5) die Website für SWI-Prolog.

Programmmodule

• (1) Erzeugung von Daten für eine gegebene Relation einer Struktur (Stelligkeit und Typ)
• (2) Einbettung einer Datenmenge in ein Modell einer gegebenen, einfachen Theorie
• (3) Approximative Einpassung einer Datenmenge in ein Modell einer einfachen Theorie
• (4) Approximative Einpassung einer Datenmenge in eine gegebene Funktion mit statistischen Methoden
• (5) Erzeugung eines Netzes mit Input, Output und Ebenen
• (6) Erklärung eines Datums durch eine einfache Theorie

Informationen zu den Modulen

Modul (1): Es kann eine Übung der Website Künstliche-Gesellschaften.de benutzt werden. Man findet die Übung indem man das Programm: «create.pl» sucht. Zusätzlich kann man im Buch 3) die Kapitel 3, 4, 6 und 12 verwenden.

Modul (2): Kapitel 3, 4, 6, 7 und 8 in 3). In 4): Kapitel 3.6 und 3.8.

Modul (3): Kapitel 3, 4, 6 und 8 in 3). In 4): Kapitel 3.9 und 3.10.

Modul (4): Kapitel 8 in 3). In 4): Kapitel 2.12, 3.9 und 3.10.

Modul (5): Kapitel 18 in 3). In 1): Kapitel 4.5.

Modul (6): Kapitel 4.10 in 4). In 1): Kapitel 1.5.

Zu allen Modulen können die zwei Beispiele in 4) konsultiert werden: Kapitel 2.8 (Stoßmechanik und Soziale Netze).

Leistungsnachweis

• eine schriftliche Arbeit (15-20 Seiten) oder
• ein 45-Minuten Vortrag, gerne auch mit Beamer. Das Thema wäre das jeweilige Simulationsmodul: der begriffliche Hintergrund und die Entwicklung des jeweiligen Programmmoduls.